Solve the following system of linear equations using Gauss-Jordan method: x + 2y + z = 7, x + 3z = 11, 2x - 3y = -1
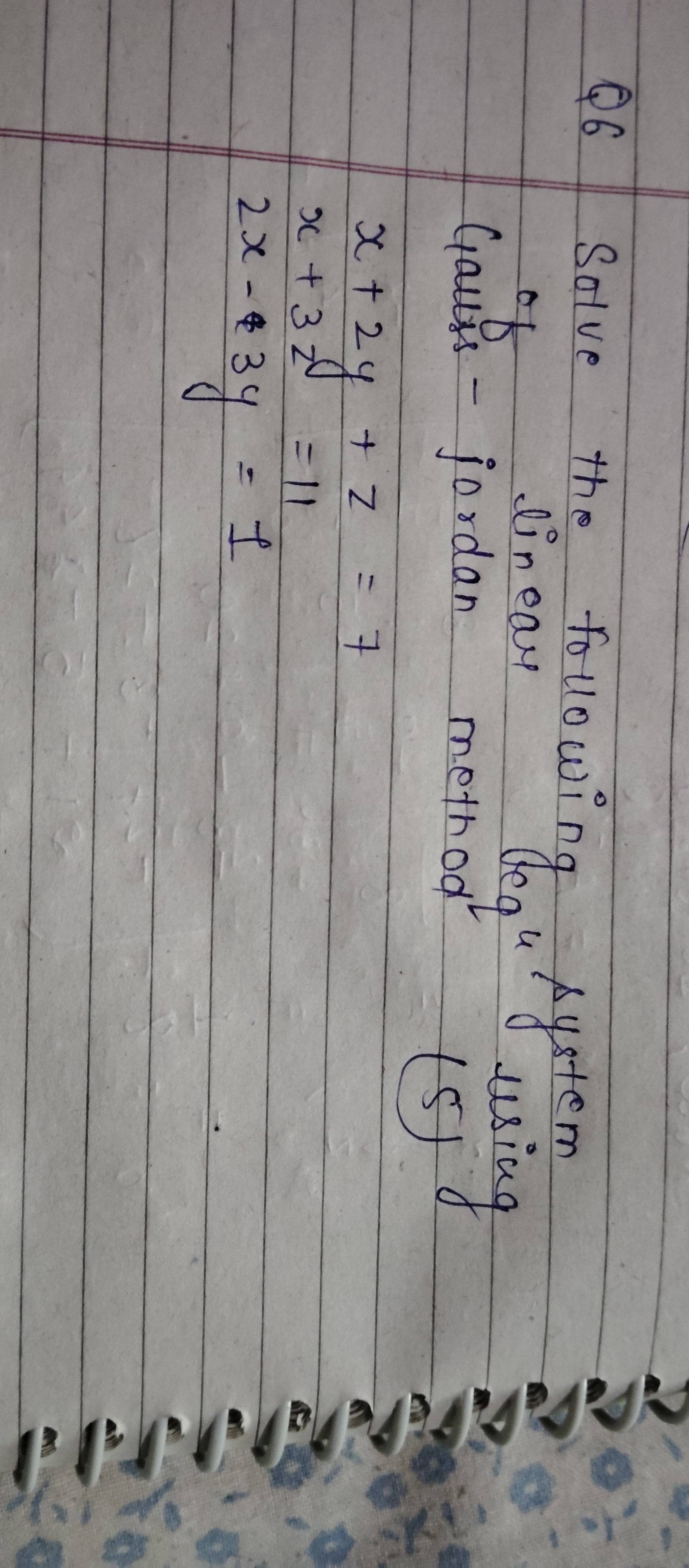
Understand the Problem
The question is asking to solve a system of linear equations using the Gauss-Jordan method. It presents three equations that need to be solved for the variables x, y, and z.
Answer
The solution is \( x = \frac{43}{5} \), \( y = -\frac{6}{5} \), \( z = \frac{4}{5} \).
Answer for screen readers
The solution to the system is:
- ( x = \frac{43}{5} )
- ( y = -\frac{6}{5} )
- ( z = \frac{4}{5} )
Steps to Solve
- Write the augmented matrix Write the augmented matrix for the system of equations:
[ \begin{bmatrix} 1 & 2 & 1 & | & 7 \ 1 & 0 & 3 & | & 11 \ 2 & -3 & 0 & | & -1 \end{bmatrix} ]
- Row operations to create leading 1s First, let's make the first column below the leading 1 (first row) into zeroes.
- Subtract the first row from the second row and subtract 2 times the first row from the third row:
[ \text{Row 2} = \text{Row 2} - \text{Row 1} = (0, -2, 2 | 4) ] [ \text{Row 3} = \text{Row 3} - 2 \times \text{Row 1} = (0, -7, -2 | -15) ]
The matrix becomes:
[ \begin{bmatrix} 1 & 2 & 1 & | & 7 \ 0 & -2 & 2 & | & 4 \ 0 & -7 & -2 & | & -15 \end{bmatrix} ]
- Eliminate the second column Next, eliminate the $-7$ in the third row. We can do this by multiplying the second row with ( \frac{7}{2} ) and adding to the third row:
[ \text{Row 3} = \text{Row 3} + \frac{7}{2} \times \text{Row 2} = (0, 0, 5 | 4) ]
The matrix updates to:
[ \begin{bmatrix} 1 & 2 & 1 & | & 7 \ 0 & -2 & 2 & | & 4 \ 0 & 0 & 5 & | & 4 \end{bmatrix} ]
- Normalize the last row Now normalize the last row by dividing by 5:
[ \text{Row 3} = \text{Row 3} \div 5 = (0, 0, 1 | \frac{4}{5}) ]
Resulting in:
[ \begin{bmatrix} 1 & 2 & 1 & | & 7 \ 0 & -2 & 2 & | & 4 \ 0 & 0 & 1 & | & \frac{4}{5} \end{bmatrix} ]
- Back substitute to find y and x Next, substitute back to find values for (y) and (x).
From Row 3:
[ z = \frac{4}{5} ]
Substituting (z) into Row 2:
[ 0y + 2 \left(\frac{4}{5}\right) = 4 \implies -2y = 4 - \frac{8}{5} \implies -2y = \frac{20}{5} - \frac{8}{5} \implies -2y = \frac{12}{5} \implies y = -\frac{6}{5} ]
Substituting (y) and (z) back into Row 1:
[ x + 2\left(-\frac{6}{5}\right) + \frac{4}{5} = 7 \implies x - \frac{12}{5} + \frac{4}{5} = 7 \implies x - \frac{8}{5} = 7 \implies x = 7 + \frac{8}{5} = \frac{35}{5} + \frac{8}{5} = \frac{43}{5} ]
Therefore, we have:
[ x = \frac{43}{5}, \quad y = -\frac{6}{5}, \quad z = \frac{4}{5} ]
The solution to the system is:
- ( x = \frac{43}{5} )
- ( y = -\frac{6}{5} )
- ( z = \frac{4}{5} )
More Information
The Gauss-Jordan elimination method systematically transforms the system into a simpler form, allowing for easier back-substitution to find the variable values. This method is effective for solving linear systems with multiple equations.
Tips
- Forgetting to apply the row operation correctly can lead to incorrect entries in the matrix.
- Neglecting to simplify fractions can cause confusion during back substitution.
AI-generated content may contain errors. Please verify critical information