€138.50 = 1000 / (1 + r)^30
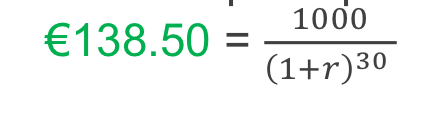
Understand the Problem
The question presents a financial equation involving a present value, an amount of €1000, and an unknown interest rate r over a period of 30 years. The goal likely involves solving for the interest rate r given the present value.
Answer
The interest rate \( r \approx 0.0820 \) or approximately \( 8.20\% \).
Answer for screen readers
The interest rate ( r \approx 0.0820 ) or approximately ( 8.20% ).
Steps to Solve
-
Set up the equation Start with the original equation given: $$ 138.50 = \frac{1000}{(1+r)^{30}} $$
-
Multiply both sides by ((1+r)^{30}) To eliminate the fraction, multiply both sides by ((1+r)^{30}): $$ 138.50 \cdot (1+r)^{30} = 1000 $$
-
Divide both sides by 138.50 To isolate ((1+r)^{30}), divide both sides by 138.50: $$ (1+r)^{30} = \frac{1000}{138.50} $$
-
Calculate the right side Now compute the right side: $$ (1+r)^{30} \approx 7.219 $$
-
Take the 30th root Next, take the 30th root of both sides to solve for (1+r): $$ 1+r = 7.219^{1/30} $$
-
Calculate (r) Subtract 1 from both sides to isolate (r): $$ r \approx 7.219^{1/30} - 1 $$
-
Compute the value of (r) Now calculate the approximate value of (r): $$ r \approx 0.0820 $$ This implies ( r \approx 8.20% ).
The interest rate ( r \approx 0.0820 ) or approximately ( 8.20% ).
More Information
This result indicates that in order to reach a present value of €138.50 after 30 years at a principal of €1000, the interest rate needs to be about 8.20%. This value can be significant when considering long-term investments and savings.
Tips
- Neglecting to compute the 30th root: Many may forget to take the root when isolating (r), leading to incorrect results.
- Rounding errors: During calculations, rounding too early can lead to inaccuracies in the final result. Always try to keep several decimal points until the final step.
AI-generated content may contain errors. Please verify critical information