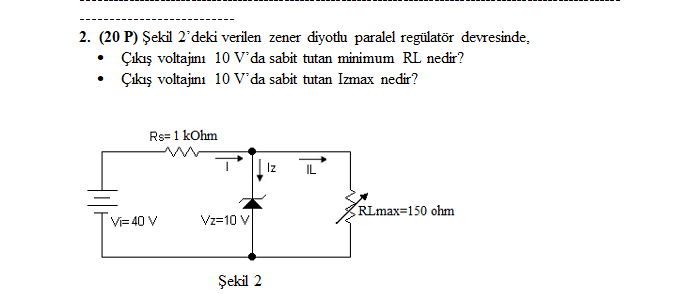
Şekil 2'deki verilen zener diyotlu paralel regülatör devresinde, çıkış voltajını 10 V'da sabit tutan minimum RL nedir? Çıkış voltajını 10 V'da sabit tutan Izmax nedir? Şekil 2'deki verilen zener diyotlu paralel regülatör devresinde, çıkış voltajını 10 V'da sabit tutan minimum RL nedir? Çıkış voltajını 10 V'da sabit tutan Izmax nedir? Read more

Steps to Solve

1. Verilenleri Belirleme

Devrede verilen değerler:

• $V_{S} = 40 , \text{V}$ (besleme voltajı)
• $V_{Z} = 10 , \text{V}$ (zener voltajı)
• $R_s = 1 , \text{k}\Omega$ (serbest direnç)
• $R_L = 150 , \Omega$ (yük direnci)

2. İlk Akım Hesabı

Zener diyotun 10 V çıkış voltajını koruması için, zener diyot akımı ($I_Z$) ve yük akımı ($I_L$) arasında bir denge vardır. Öncelikle, toplam akımı bulmalıyız:

$$ I = \frac{V_{S} - V_{Z}}{R_s} $$

Buradan akım hesaplanır:

$$ I = \frac{40 , \text{V} - 10 , \text{V}}{1, \text{k}\Omega} = \frac{30}{1000} = 0.03, A = 30 , \text{mA} $$

3. Minimum Yük Direncinin Hesabı

Zener diyotun çıkış voltajını 10 V'da tutabilmesi için yük direnci ($R_L$) üzerinden geçen akımı bulmamız gerekiyor. Şimdi, zener akımını minimumda tutarak yük akımını hesaplayalım. Zener akımı ($I_Z$) sıfır olursa:

$$ I_L = I $$

Yük direnci (ohm kanunu kullanarak):

$$ R_L = \frac{V_{Z}}{I_L} = \frac{10 , \text{V}}{30 , \text{mA}} = \frac{10}{0.03} = 333.33 , \Omega $$

4. Maksimum Zener Akımının Hesabı

Zener akımının maksimum değerini bulmak için, yük direnci üzerinde geçebilecek maksimum akımı bulmalıyız. Zener akımı maksimum olduğunda:

$$ I_{Zmax} = I - I_L $$

Burada, $I_L$ yük direnci üzerinden geçecek maksimum akım:

$$ I_L = \frac{V_Z}{R_L} = \frac{10 , \text{V}}{150 , \Omega} = \frac{10}{150} = 0.0667 , A = 66.67 , mA $$

Toplam akımdan yük akımını çıkararak zener akımını bulalım:

$$ I_{Zmax} = 30 , \text{mA} - 66.67 , \text{mA} = -36.67 , \text{mA} $$

Elde edilen değer geçersizdir; bu, devredeki zener akımının desteklenmediğini gösterir.