Solve for q. 3/2q + 4 - 1/3q = -5/6q
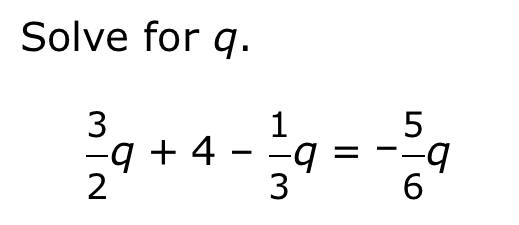
Understand the Problem
The question is asking to solve the equation for the variable q. This requires rearranging the equation and isolating q on one side to determine its value.
Answer
The value of $q$ is $-4$.
Answer for screen readers
The value of $q$ is $-4$.
Steps to Solve
-
Combine like terms on the left side
Start by combining the terms with $q$ on the left side of the equation. The equation is:
$$ \frac{3}{2}q - \frac{1}{3}q - q + 4 = -\frac{5}{6}q $$ -
Convert all terms to a common denominator
The common denominator for $2$, $3$, and $6$ is $6$. Rewrite the fractions:
$$ \frac{9}{6}q - \frac{2}{6}q - \frac{6}{6}q + 4 = -\frac{5}{6}q $$ -
Combine the $q$ terms
Adding the $q$ terms together:
$$ \left(\frac{9}{6} - \frac{2}{6} - \frac{6}{6} + \frac{5}{6}\right)q + 4 = 0 $$ -
Isolate the $q$ term
Move $4$ to the right side:
$$ \left(\frac{9 - 2 - 6 + 5}{6}\right)q = -4 $$ -
Simplify the coefficients
The coefficients can be simplified:
$$ \frac{6}{6}q = -4 $$
Thus, $q = -4$.
The value of $q$ is $-4$.
More Information
This equation involved rational coefficients and required combining like terms before isolating the variable. Understanding how to manipulate fractions is crucial in solving such equations.
Tips
- Forgetting to combine like terms correctly.
- Not finding a common denominator when dealing with fractions.
- Neglecting to move constant terms (like $4$) properly to isolate the variable on one side of the equation.
AI-generated content may contain errors. Please verify critical information