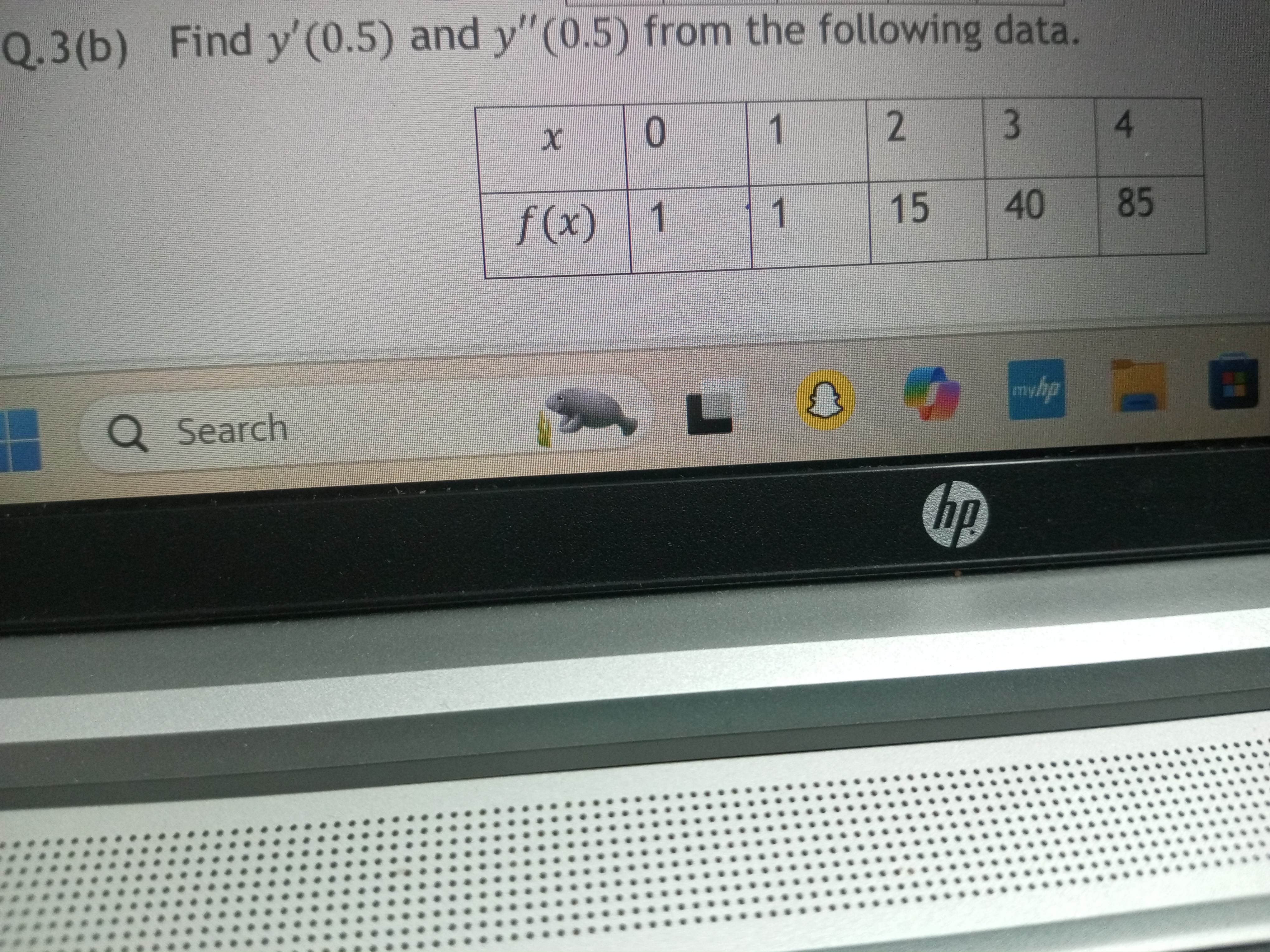
Find y'(0.5) and y''(0.5) from the following data.
Understand the Problem
The question is asking to find the first and second derivatives of a function at the point x = 0.5 using the provided data in the table.
Answer
$y'(0.5) = 0$, $y''(0.5) = 14$
Answer for screen readers
The first derivative at ( x = 0.5 ) is ( y'(0.5) = 0 ), and the second derivative at ( x = 0.5 ) is ( y''(0.5) = 14 ).
Steps to Solve
- Understanding the Data Points
We are given discrete values for ( x ) and ( f(x) ): [ \begin{array}{|c|c|} \hline x & f(x) \ \hline 0 & 1 \ 1 & 1 \ 2 & 15 \ 3 & 40 \ 4 & 85 \ \hline \end{array} ]
- Calculate the First Derivative ( y'(0.5) )
To estimate ( y'(0.5) ), we can use the average rate of change between the points around ( x = 0.5 ). We can use points ( (0, f(0)) ) and ( (1, f(1)) ).
The formula for the derivative is: [ y'(x) \approx \frac{f(x+h) - f(x)}{h} ] For ( x = 0 ) and ( h = 1 ): [ y'(0.5) \approx \frac{f(1) - f(0)}{1 - 0} = \frac{1 - 1}{1} = 0 ]
- Calculating the Second Derivative ( y''(0.5) )
For the second derivative ( y''(0.5) ), we use the same points to find the derivatives again. We will consider the changes in the slope computed earlier. We can use points ( (0, f(0)) ), ( (1, f(1)) ), and ( (2, f(2)) ).
Using the formula: [ y''(x) \approx \frac{y'(x+h) - y'(x)}{h} ]
First, we need to calculate ( y'(1) ) using points ( (1, f(1)) ) and ( (2, f(2)) ): [ y'(1) \approx \frac{f(2) - f(1)}{2 - 1} = \frac{15 - 1}{1} = 14 ]
Next, we calculate ( y''(0.5) ) using ( y'(0) ) and ( y'(1) ): [ y''(0.5) \approx \frac{y'(1) - y'(0)}{1 - 0} = \frac{14 - 0}{1} = 14 ]
The first derivative at ( x = 0.5 ) is ( y'(0.5) = 0 ), and the second derivative at ( x = 0.5 ) is ( y''(0.5) = 14 ).
More Information
The derivatives estimate how the function behaves at a certain point. The first derivative ( y'(0.5) ) shows that the function is flat at this point, while ( y''(0.5) ) indicates the acceleration of the function's rate of change, suggesting an upward curve.
Tips
- Confusing the use of ( f(x) ) with ( f'(x) ) or ( f''(x) ). Always ensure you're differentiating correctly based on the values given.
- Not using surrounding points for derivative calculations. It’s essential to balance points around the value of interest for a better estimate.
AI-generated content may contain errors. Please verify critical information