lim x→1- (ln x / (x - 1))^(1/(1 - x)) limitinin sonucu aşağıdakilerden hangisidir?
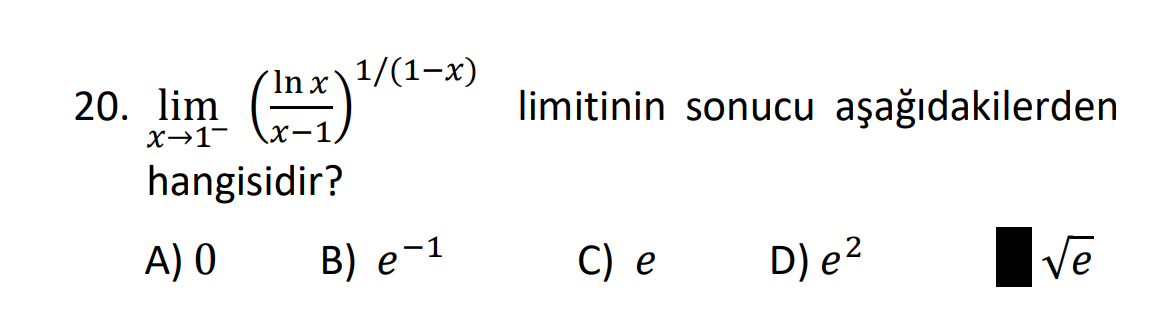
Understand the Problem
Bu soru, x 1'e yaklaşırken verilen limit ifadesinin sonucunu bulmamızı istemektedir. Limit hesaplama tekniklerini uygulayarak sonucu belirleyeceğiz.
Answer
Limitin sonucu $1$.
Answer for screen readers
Limitin sonucu $1$.
Steps to Solve
- Limit ifadesini yeniden düzenleme
Verilen limit ifadesini $x \to 1^{-}$ olarak değerlendireceğiz. İlk adımda, bu ifadeyi limitin formunu daha kolay hale getirecek biçimde düzenleyelim:
$$ y = \left(\frac{\ln x}{x - 1}\right)^{\frac{1}{1 - x}} $$
- Logaritmik dönüşüm kullanma
Limit ifadesinde $1 - x$ şeklinde bir kesir olduğundan, bu durumu daha iyi anlamak için logaritma alarak dönüşüm yapabiliriz. Logaritma özelliği gereği:
$$ \ln y = \frac{1}{1 - x} \ln\left(\frac{\ln x}{x - 1}\right) $$
- Limit içindeki bileşenlerin durumu
Şimdi, $x \to 1^{-}$ için $\ln x \to \ln 1 = 0$ ve $x - 1 \to 0^{-}$ olacaktır. Buradan yola çıkarak, limit ifadesinin iki bileşenine bakmalıyız:
- $\ln x = \ln(1 + (x-1)) \to 0$
- $x - 1 \to 0^{-}$
Bunları birleştirerek:
$$ \lim_{x \to 1^{-}} \frac{\ln x}{x - 1} $$
Bu limitin L'Hôpital kuralı ile hesaplanması gerekir:
- L'Hôpital kuralı kullanma
L'Hôpital kuralına göre limitimizi hesaplayalım:
$$ \lim_{x \to 1^{-}} \frac{\ln x}{x - 1} = \lim_{x \to 1^{-}} \frac{\frac{d}{dx}(\ln x)}{\frac{d}{dx}(x - 1)} = \lim_{x \to 1^{-}} \frac{\frac{1}{x}}{1} = \frac{1}{1} = 1 $$
- Sonuç olarak logaritmaya geri dönme
Şimdi, bu sonucu kullanarak:
$$ \ln y = \frac{1}{1-x} \ln(1) = 0 $$
Bu durumda $y = e^0 = 1$ olur.
- Son limitin hesaplanması
Şimdi bu değeri kullanarak asıl limitimize dönebiliriz:
$$ y \to 1 $$
Bu yüzden limitin sonucu:
$$ \lim_{x \to 1^{-}} y = \lim_{x \to 1^{-}} 1 = 1 $$
Limitin sonucu $1$.
More Information
Verilen limit ifadesinin sonucu 1'dir. Bu ifade, L'Hôpital kuralı ve logaritmik dönüşümler kullanılarak analiz edildi. Ayrıca, limitin sonucu doğrudan 0 olan bir form içermediği için dikkatlice ele alınmalıdır.
Tips
- L'Hôpital kuralı yanlış uygulaması: Limitin $0/0$ veya $\infty/\infty$ formlarında doğru kullanılmasına dikkat edilmelidir.
- Logaritmik dönüşümde $\ln(1)$'in sıfır olduğu unutulmamalıdır.
AI-generated content may contain errors. Please verify critical information