How do you analyze the circuit shown in the image?
Understand the Problem
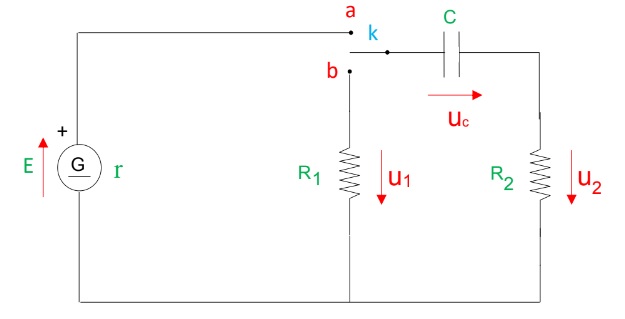
The question is likely asking how to analyze an electrical circuit involving resistors, a capacitor, and an electromotive force (EMF). It invites a discussion about voltage and current relationships in the circuit, including how to apply Kirchhoff's laws.
Answer
The differential equation for the circuit is given by $E - I_1 R_1 - \frac{q}{C} - I_2 R_2 = 0$.
Answer for screen readers
The relationship derived from the circuit analysis can be expressed using the differential equation:
$$ E - I_1 R_1 - \frac{q}{C} - I_2 R_2 = 0 $$
Steps to Solve
- Identify the Components and Connections
In the circuit, identify the components: a voltage source (EMF $E$), a resistor $R_1$, a capacitor $C$, and a second resistor $R_2$. Note the points $a$, $b$, and $k$ indicating connection points.
- Apply Kirchhoff's Voltage Law
Use Kirchhoff's Voltage Law (KVL), which states that the sum of the electrical potential differences (voltage) around any closed circuit loop must equal zero.
For the loop $E - U_1 - U_C - U_2 = 0$, we can express the voltages as:
$$ E - U_1 - U_C - U_2 = 0 $$
- Express Voltages in Terms of Currents and Resistances
From Ohm's Law, we know that the voltage across a resistor is given by $U = IR$, where $I$ is the current through the resistor. Therefore, we can express $U_1$ and $U_2$ as:
$$ U_1 = I_1 R_1 $$
$$ U_2 = I_2 R_2 $$
- Consider Capacitor Voltage Relation
The voltage across the capacitor $C$ is given by:
$$ U_C = \frac{q}{C} $$
where $q$ is the charge stored in the capacitor. The relationship between current $I$ and charge $q$ is defined as:
$$ I = \frac{dq}{dt} $$
- Set Up the Differential Equation
Substituting for $U_1$, $U_2$, and $U_C$ into the KVL equation gives:
$$ E - I_1 R_1 - \frac{q}{C} - I_2 R_2 = 0 $$
This forms the basis for a differential equation that describes the circuit's behavior over time.
The relationship derived from the circuit analysis can be expressed using the differential equation:
$$ E - I_1 R_1 - \frac{q}{C} - I_2 R_2 = 0 $$
More Information
This equation captures the interplay between the current, voltage, and charge in the circuit. Such analyses are crucial in understanding how circuits respond to differing conditions, particularly in AC and transient analysis.
Tips
- Forgetting Kirchhoff's Law: Failing to apply Kirchhoff's laws can lead to incomplete equations.
- Misapplying Ohm’s Law: Always account for the right resistances and currents in Ohm's Law.
- Ignoring Capacitor Dynamics: Not considering how the charge on the capacitor influences the voltage can lead to incorrect conclusions.
AI-generated content may contain errors. Please verify critical information