How many chairs will Rachel place around each table at her birthday party?
Understand the Problem
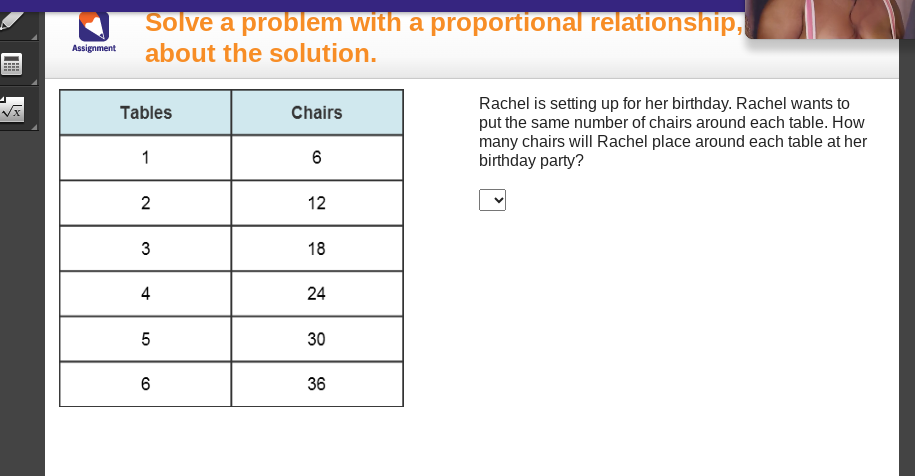
The question is asking how many chairs Rachel will place around each table at her birthday party, given a proportional relationship between the number of tables and chairs shown in the provided data. We need to identify the consistent pattern that determines the number of chairs based on the number of tables.
Answer
Rachel will place 6 chairs around each table at her birthday party.
Answer for screen readers
Rachel will place 6 chairs around each table at her birthday party.
Steps to Solve
- Identify the Pattern
First, look at the data provided in the table. We can observe how the number of chairs increases as the number of tables increases.
- Determine the Ratio
Calculate the ratio of chairs to tables. From the table:
- For 1 table, 6 chairs: $\frac{6}{1} = 6$
- For 2 tables, 12 chairs: $\frac{12}{2} = 6$
- For 3 tables, 18 chairs: $\frac{18}{3} = 6$
This shows a consistent ratio of 6 chairs per table.
- Calculate Chairs for Any Number of Tables
Using the identified ratio, determine the number of chairs for any given number of tables by multiplying the number of tables by the ratio:
- Formula: Number of chairs = Number of tables $\times 6$
- Find Chairs for 6 Tables
Substituting the number of tables into the formula: $$ \text{Chairs} = 6 \text{ (tables)} \times 6 = 36 $$
Rachel will place 6 chairs around each table at her birthday party.
More Information
The relationship between the number of tables and chairs is linear, with the number of chairs increasing by a fixed amount (6) for each additional table. This represents a proportional relationship.
Tips
- Misinterpreting the data by not recognizing the constant ratio between the tables and chairs.
- Forgetting to multiply the ratio correctly to find the number of chairs for a specific number of tables.
AI-generated content may contain errors. Please verify critical information