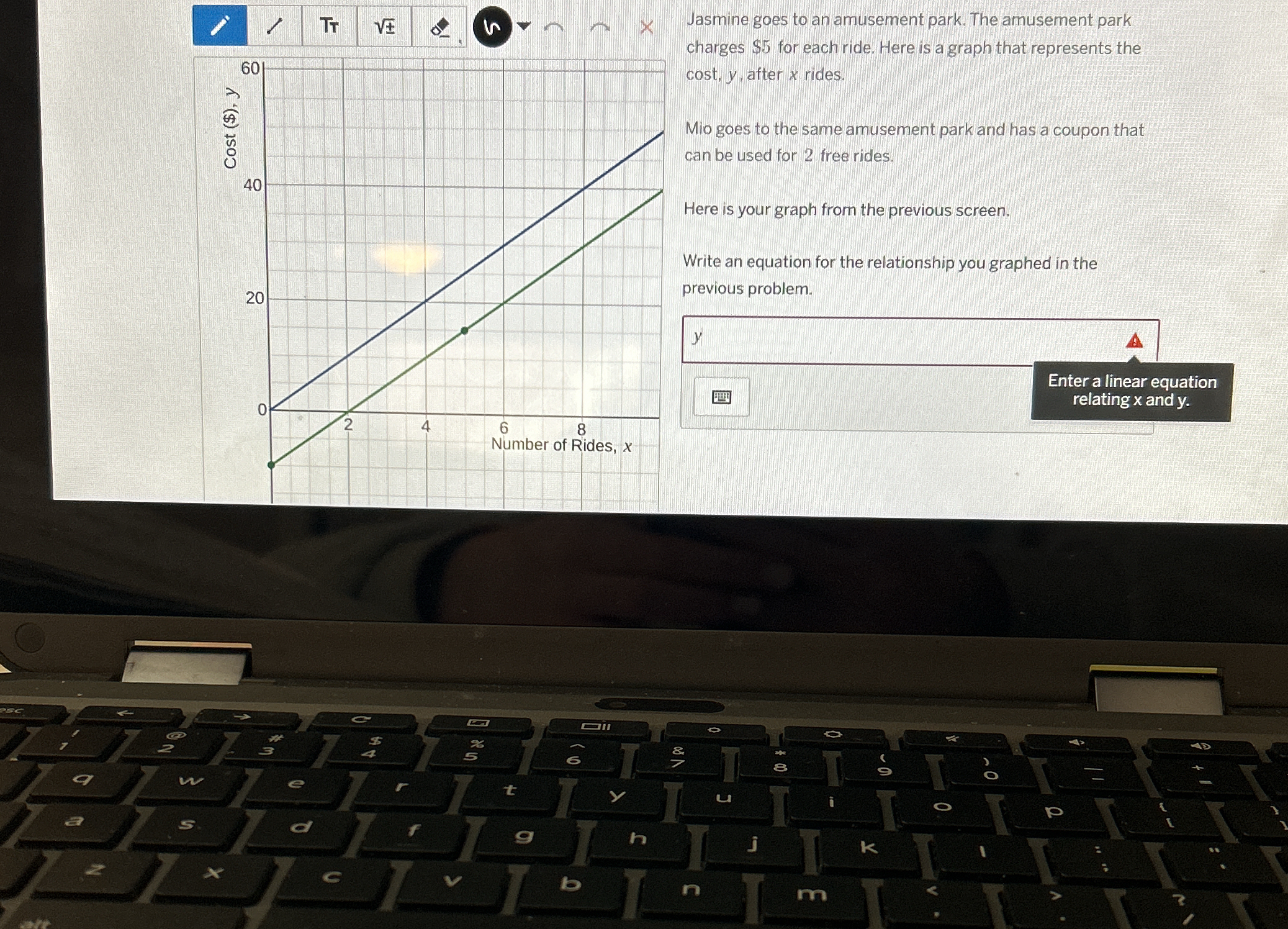
Write an equation for the relationship you graphed in the previous problem.
Understand the Problem
The question is asking to write a linear equation that represents the relationship between the number of rides (x) and the cost (y) at an amusement park, as initially provided in the problem context.
Answer
$$ y = 5x $$
Answer for screen readers
The linear equation representing the relationship is: $$ y = 5x $$
Steps to Solve
-
Identify the Slope The slope of the line represents the cost per ride. From the problem, the amusement park charges $5 for each ride. Thus, the slope $m$ is: $$ m = 5 $$
-
Determine the Y-Intercept The y-intercept represents the initial cost when no rides are taken, which is $0. Therefore, the y-intercept $b$ is: $$ b = 0 $$
-
Formulate the Linear Equation Using the slope-intercept form of the linear equation, which is given by: $$ y = mx + b $$ we substitute the values of $m$ and $b$: $$ y = 5x + 0 $$
-
Simplify the Equation Since adding zero does not change the value, we can simplify the equation to: $$ y = 5x $$
The linear equation representing the relationship is: $$ y = 5x $$
More Information
This equation indicates that for every ride, the cost increases by $5. If you take $x$ rides, the total cost is $5$ times the number of rides.
Tips
- Forgetting to include the y-intercept: Always check if there is a starting cost.
- Miscalculating the slope: Ensure you define it based on the problem context correctly.
AI-generated content may contain errors. Please verify critical information