Simplify the expression (x + y)/(x - y) - (x - y)/(x + y)
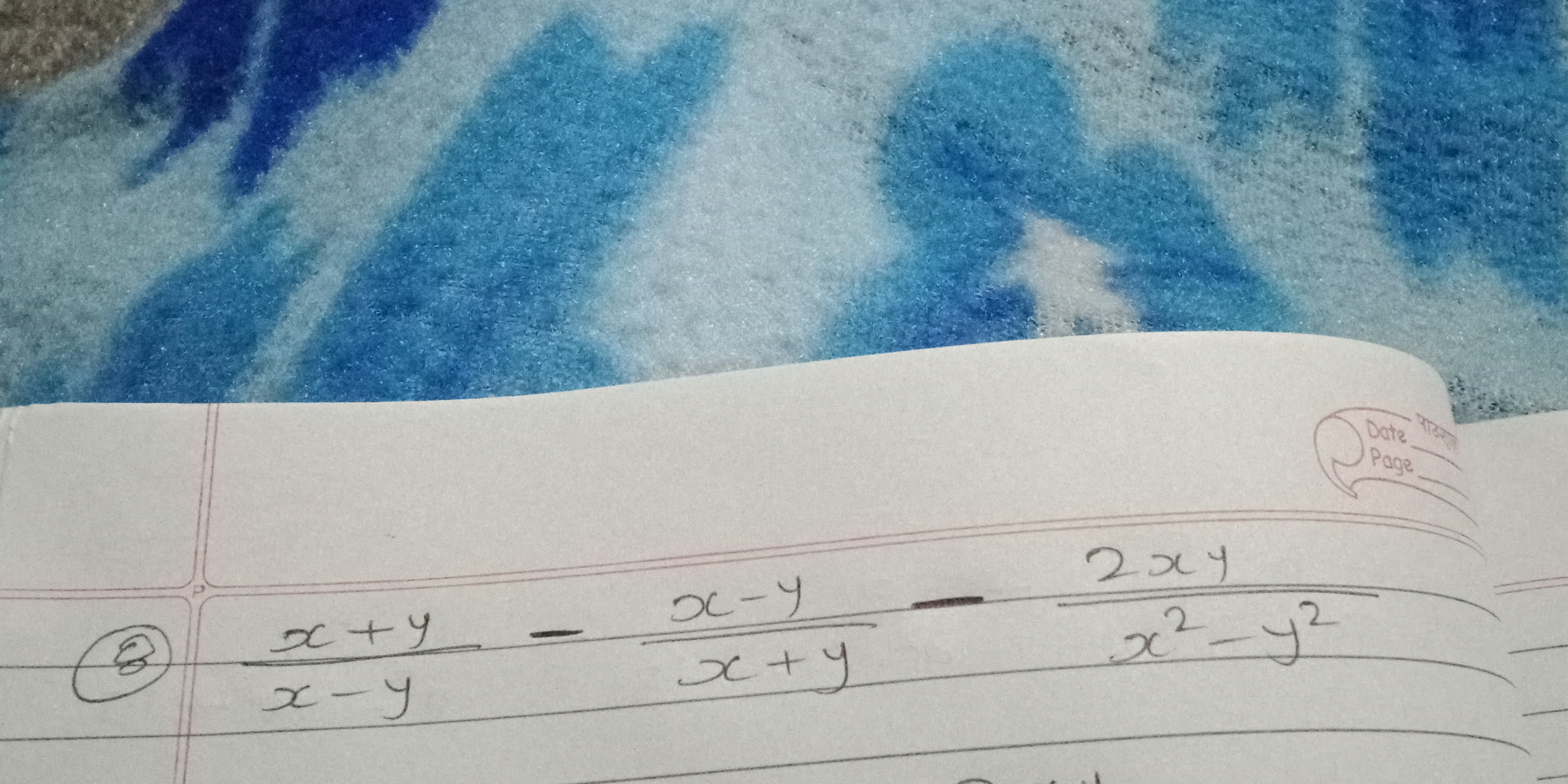
Understand the Problem
The question is asking to simplify an expression involving algebraic fractions. It appears that there are two fractions to be simplified by performing algebraic operations, particularly subtraction and potentially factorization.
Answer
The simplified expression is $$ \frac{4xy}{(x-y)(x+y)} $$
Answer for screen readers
The simplified expression is
$$ \frac{4xy}{(x-y)(x+y)} $$
Steps to Solve
- Identify the expression to simplify
The expression given is:
$$ \frac{x+y}{x-y} - \frac{x-y}{x+y} $$
- Find a common denominator
The common denominator for both fractions is $(x-y)(x+y)$. Rewrite each fraction:
$$ \frac{(x+y)(x+y)}{(x-y)(x+y)} - \frac{(x-y)(x-y)}{(x-y)(x+y)} $$
- Simplify the numerators
Now simplify the numerators:
1st fraction:
$$ (x+y)^2 = x^2 + 2xy + y^2 $$
2nd fraction:
$$ (x-y)^2 = x^2 - 2xy + y^2 $$
Thus, we rewrite the expression as:
$$ \frac{(x^2 + 2xy + y^2) - (x^2 - 2xy + y^2)}{(x-y)(x+y)} $$
- Combine the numerators
Now combine the numerators:
$$ x^2 + 2xy + y^2 - x^2 + 2xy - y^2 = 4xy $$
The expression simplifies to:
$$ \frac{4xy}{(x-y)(x+y)} $$
- Final check for further simplification
We can observe that the numerator has no common factors with the denominator, so this is the simplest form.
The simplified expression is
$$ \frac{4xy}{(x-y)(x+y)} $$
More Information
This expression represents the result of subtracting two algebraic fractions. It can be useful in various algebraic contexts, particularly in simplifying rational expressions and solving equations involving fractions.
Tips
- Forgetting to find a common denominator when subtracting fractions.
- Not simplifying the numerator correctly after expanding expressions.
- Overlooking that the final expression cannot be simplified further.
AI-generated content may contain errors. Please verify critical information