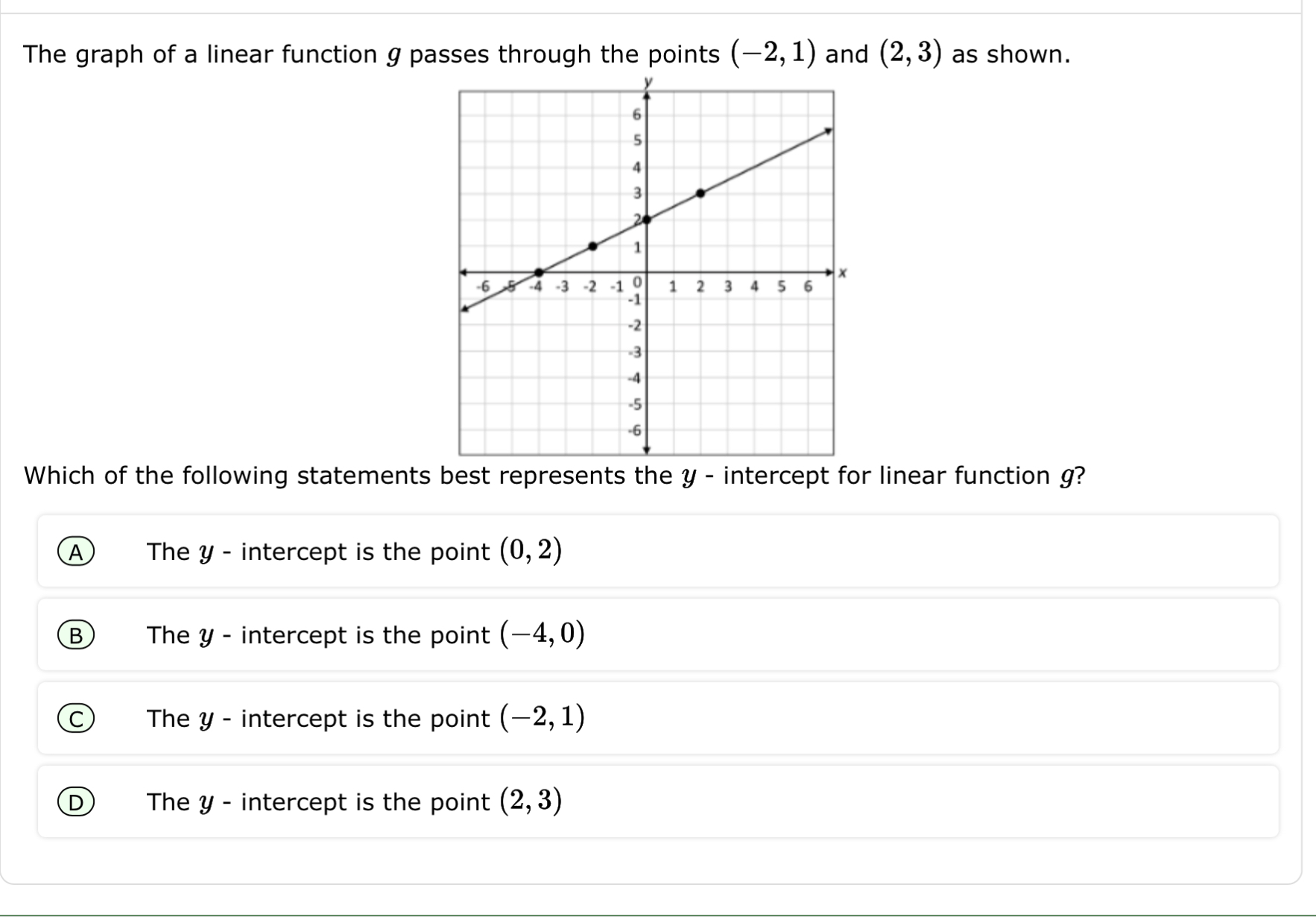
Which of the following statements best represents the y-intercept for linear function g?

Steps to Solve

1. Understand the y-intercept The y-intercept of a linear function is the point where the line crosses the y-axis. This occurs when $x = 0$.

2. Identify the points on the graph The graph passes through the points $(-2, 1)$ and $(2, 3)$. We can use these points to find the equation of the line.

3. Calculate the slope of the line The slope $m$ can be calculated using the formula:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Substituting in our points, we have:

$$ m = \frac{3 - 1}{2 - (-2)} = \frac{2}{4} = \frac{1}{2} $$

4. Use point-slope form to find the line's equation Using one of the points, say $(2, 3)$, we can apply the point-slope form of a line:

$$ y - y_1 = m(x - x_1) $$

Substituting in gives:

$$ y - 3 = \frac{1}{2}(x - 2) $$

Simplifying this:

$$ y - 3 = \frac{1}{2}x - 1 $$

$$ y = \frac{1}{2}x + 2 $$

5. Determine the y-intercept from the equation From the simplified equation $y = \frac{1}{2}x + 2$, we see that the y-intercept is $2$. Thus, the point is $(0, 2)$.