Find the value of f^(n)(x), if f(x) = x / ((x - 1)(x - 2))
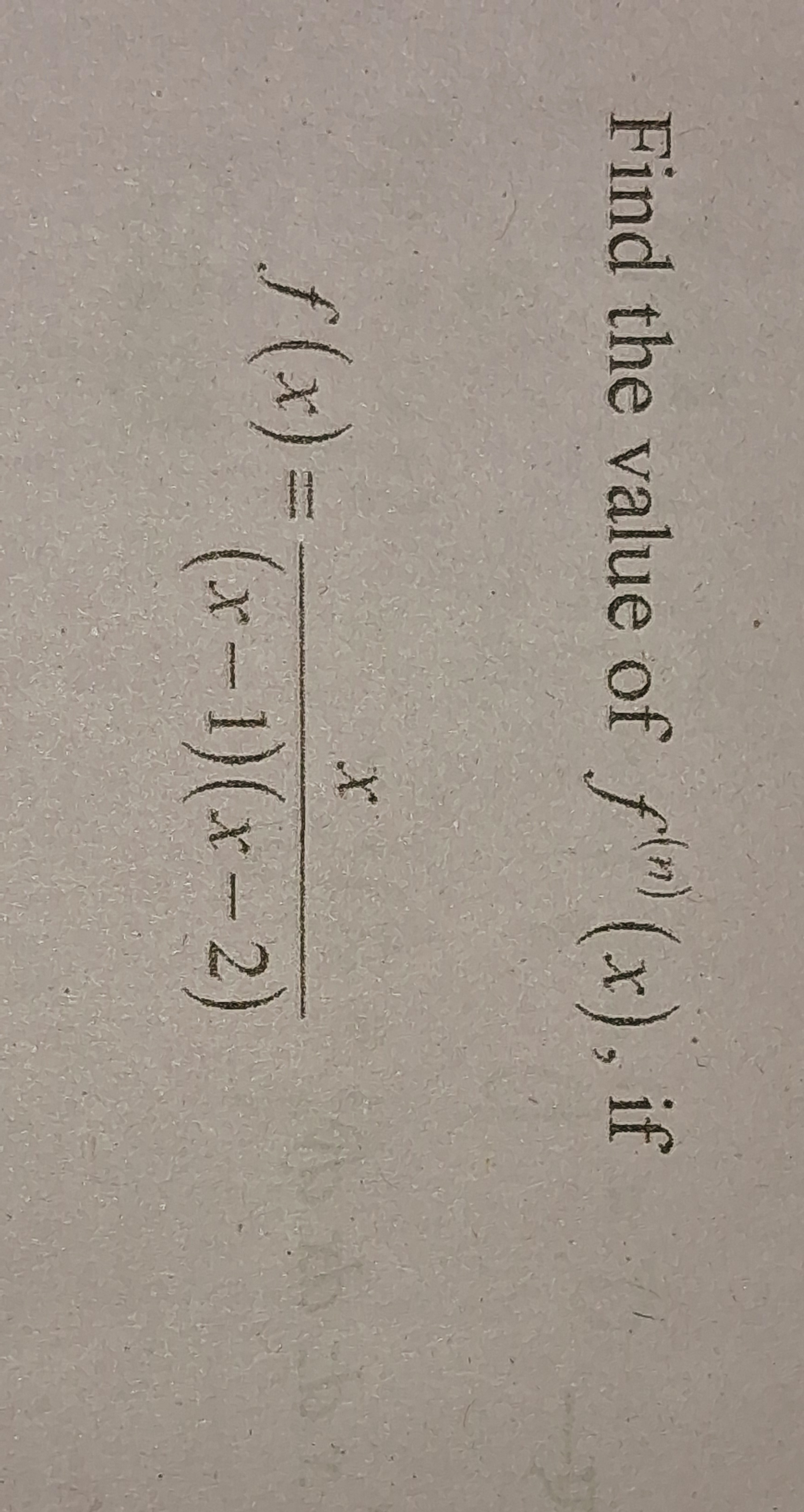
Understand the Problem
The question is asking to find the value of the n-th derivative of the function f(x) given in the image. This involves analyzing the function's form and potentially applying derivative rules to solve.
Answer
The value of \( f^{(n)}(x) \) will depend on patterns discovered in the derivatives, expressed as a formula based on prior derivatives.
Answer for screen readers
The value of ( f^{(n)}(x) ) will depend on the specific structure identified from computed derivatives:
$$ f^{(n)}(x) \text{ can be obtained from a recurrence relation or explicit formula derived from the first few derivatives.} $$
Steps to Solve
-
Identify the function and its components
The function is given as ( f(x) = \frac{x}{(x - 1)(x - 2)} ). We can recognize that it is a rational function, which may be analyzed for derivatives. -
Simplify the function (if necessary)
Before calculating higher-order derivatives, we can perform polynomial long division or partial fraction decomposition, but it is not necessary for this function as we can derive it directly. -
Compute the first derivative using the quotient rule
The quotient rule states that for ( \frac{u}{v} ), the derivative is given by:
$$ f'(x) = \frac{u'v - uv'}{v^2} $$
Here, ( u = x ) and ( v = (x - 1)(x - 2) ). -
Differentiate explicitly
Let’s compute the first derivative components:
- ( u' = 1 )
- ( v' = (x - 1) + (x - 2) = 2x - 3 )
Thus, applying the quotient rule:
$$ f'(x) = \frac{(1)((x - 1)(x - 2)) - (x)(2x - 3)}{((x - 1)(x - 2))^2} $$
-
General form for n-th derivative
For rational functions, the ( n )-th derivative can often be simplified using relationships discovered in earlier derivatives or using the properties of derivatives in rational functions. The derivatives tend to follow a pattern which can be derived from the first few derivatives calculated. -
Identify patterns in derivatives
Continuing this process can be very complex, so one might notice that the results for ( f^{(n)}(x) ) will depend heavily on the structure of the function. -
Conclusions based on patterns
After finding the first few derivatives, we can extrapolate to express ( f^{(n)}(x) ) in a general form.
The value of ( f^{(n)}(x) ) will depend on the specific structure identified from computed derivatives:
$$ f^{(n)}(x) \text{ can be obtained from a recurrence relation or explicit formula derived from the first few derivatives.} $$
More Information
Rational functions often have derivatives that express a pattern. The first few derivatives can allow you to derive more general forms without calculating each derivative manually, making it efficient for determining higher-order derivatives.
Tips
- Not applying the quotient rule correctly when differentiating rational functions.
- Forgetting to simplify the derivatives step-by-step, which could lead to errors.
- Overlooking the possibility of recurrence relations for the derivatives of rational functions.
AI-generated content may contain errors. Please verify critical information