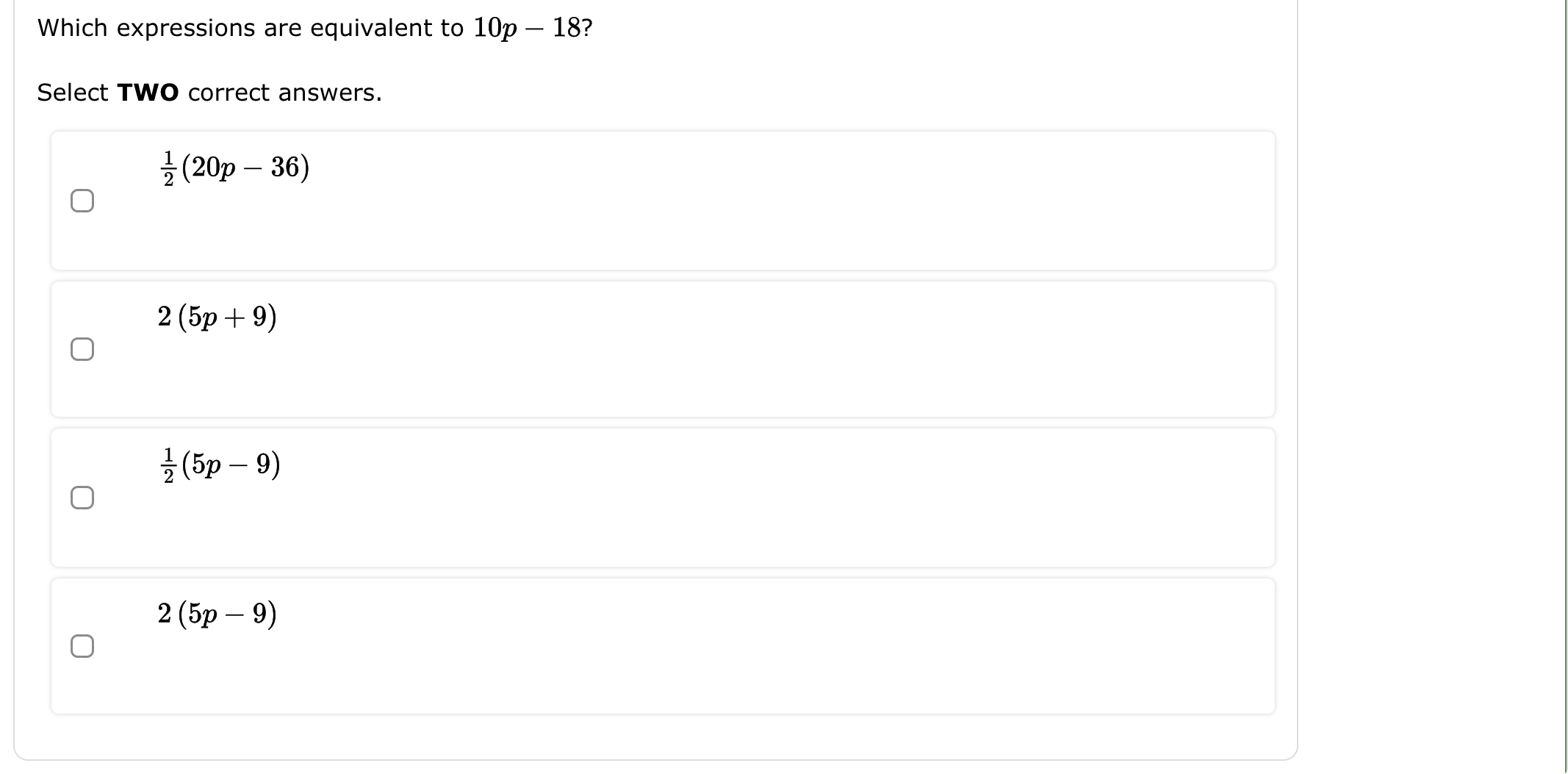
Which expressions are equivalent to 10p - 18? Select TWO correct answers.

Steps to Solve

1. Understand the Original Expression The original expression is $10p - 18$. We need to simplify the answer choices to see if they can be rewritten to match this expression.

2. Evaluate the First Expression For the expression $\frac{1}{2}(20p - 36)$:

   • Distribute $\frac{1}{2}$: $$ \frac{1}{2} \cdot 20p - \frac{1}{2} \cdot 36 = 10p - 18 $$ This matches the original expression.

3. Evaluate the Second Expression For the expression $2(5p + 9)$:

   • Distribute $2$: $$ 2 \cdot 5p + 2 \cdot 9 = 10p + 18 $$ This does not match the original expression.

4. Evaluate the Third Expression For the expression $\frac{1}{2}(5p - 9)$:

   • Distribute $\frac{1}{2}$: $$ \frac{1}{2} \cdot 5p - \frac{1}{2} \cdot 9 = \frac{5}{2}p - \frac{9}{2} $$ This does not match the original expression.

5. Evaluate the Fourth Expression For the expression $2(5p - 9)$:

   • Distribute $2$: $$ 2 \cdot 5p - 2 \cdot 9 = 10p - 18 $$ This matches the original expression.

6. Evaluate the Fifth Expression For the expression $2(5p)$:

   • Distributing isn't necessary here as it's not in the form needing transformation.
   • This simplification is necessary for comparison, determining $2(5p - 9)$ is already simplified.

7. Final Comparison The expressions equivalent to $10p - 18$ are $\frac{1}{2}(20p - 36)$ and $2(5p - 9)$.