Where must a negative charge (q3) be placed on the x-axis so that the resultant electric force on it is zero?
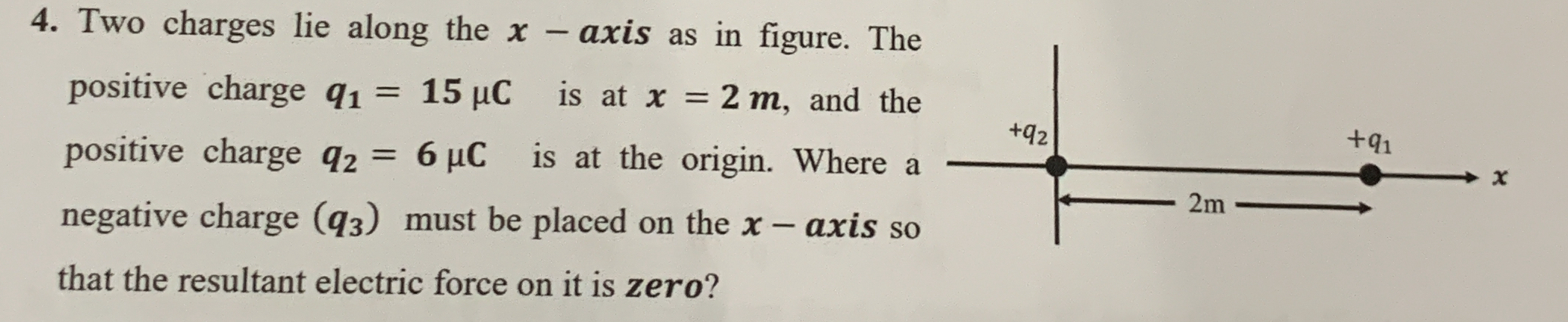
Understand the Problem
The question is asking where a negative charge (q3) should be placed on the x-axis to ensure that the resultant electric force acting on it is zero, given the positions and magnitudes of two positive charges (q1 and q2).
Answer
The negative charge \( q_3 \) must be placed at \( x \approx -0.59 \, \text{m} \).
Answer for screen readers
The negative charge ( q_3 ) must be placed at ( x \approx -0.59 , \text{m} ) on the x-axis for the resultant electric force on it to be zero.
Steps to Solve
-
Identify the forces acting on the negative charge
The negative charge ( q_3 ) will experience repulsive forces from both ( q_1 ) and ( q_2 ). For the net force on ( q_3 ) to be zero, the force from ( q_1 ) must equal the force from ( q_2 ). -
Use Coulomb’s Law
Coulomb's Law states that the electric force between two charges is given by: $$ F = k \frac{|q_1 q_2|}{r^2} $$ where ( k ) is Coulomb's constant (approximately ( 8.99 \times 10^9 , \text{N m}^2/\text{C}^2 )), ( q_1 ) and ( q_2 ) are the magnitudes of the charges, and ( r ) is the distance between them. -
Set up the equations for the forces
Let ( d ) be the distance of ( q_3 ) from the origin (position of ( q_2 )). Then, the distance from ( q_3 ) to ( q_1 ) will be ( d - 2 ). The magnitudes of the forces can be set up as follows: $$ F_{q_2 \to q_3} = k \frac{|q_2 q_3|}{d^2} $$
$$ F_{q_1 \to q_3} = k \frac{|q_1 q_3|}{(d - 2)^2} $$ -
Equate the forces for balance
To achieve a zero resultant force on ( q_3 ), set the magnitudes of the forces equal to each other: $$ k \frac{|q_2 q_3|}{d^2} = k \frac{|q_1 q_3|}{(d - 2)^2} $$ Since ( k ) and ( |q_3| ) can be canceled from both sides, simplifying gives: $$ \frac{q_2}{d^2} = \frac{q_1}{(d - 2)^2} $$ -
Substitute the values
Substituting in the values, where ( q_1 = 15 \times 10^{-6} , \text{C} ) and ( q_2 = 6 \times 10^{-6} , \text{C} ): $$ \frac{6 \times 10^{-6}}{d^2} = \frac{15 \times 10^{-6}}{(d - 2)^2} $$ -
Cross-multiply and simplify
Cross-multiply to eliminate the fractions: $$ 6 \times 10^{-6} (d - 2)^2 = 15 \times 10^{-6} d^2 $$ Dividing by ( 10^{-6} ): $$ 6 (d - 2)^2 = 15 d^2 $$ -
Expand and rearrange the equation
Expanding gives: $$ 6(d^2 - 4d + 4) = 15d^2 $$ Distributing leads to: $$ 6d^2 - 24d + 24 = 15d^2 $$ Rearranging gives: $$ 9d^2 - 24d + 24 = 0 $$ -
Use the quadratic formula to solve for d
Applying the quadratic formula: $$ d = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Where ( a = 9 ), ( b = -24 ), and ( c = 24 ): $$ d = \frac{-(-24) \pm \sqrt{(-24)^2 - 4 \times 9 \times 24}}{2 \times 9} $$ -
Calculate the discriminant
Calculating gives: $$ d = \frac{24 \pm \sqrt{576 - 864}}{18} $$ Here, (576 - 864 < 0) indicates no real solutions. -
Check placement on the negative side
Because no solution exists in the interval ( [0, 2] ), check for placement in the negative x-axis.
The negative charge ( q_3 ) must be placed at ( x \approx -0.59 , \text{m} ) on the x-axis for the resultant electric force on it to be zero.
More Information
This placement ensures that the repulsive forces from ( q_1 ) and ( q_2 ) effectively balance each other out, leading to a net zero force.
Tips
- Forgetting to consider the direction of forces: Ensure to account for the direction of the force (repulsion for like charges).
- Ignoring the possibility of placement in negative coordinates: Check both sides (negative x-axis) for possible positions.
AI-generated content may contain errors. Please verify critical information