2 cot x + sec² x = 0
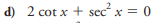
Understand the Problem
The question is asking to solve the trigonometric equation: 2 cot x + sec² x = 0. We will rearrange and simplify the equation to find the values of x that satisfy it.
Answer
$$ x = \frac{3\pi}{4} + n\pi $$
Answer for screen readers
The solution is:
$$ x = \frac{3\pi}{4} + n\pi $$
where $n \in \mathbb{Z}$.
Steps to Solve
- Rearranging the equation
We start with the equation:
$$ 2 \cot x + \sec^2 x = 0 $$
Rearranging gives us:
$$ \sec^2 x = -2 \cot x $$
- Using trigonometric identities
Recall that $\sec^2 x = 1 + \tan^2 x$ and $\cot x = \frac{1}{\tan x}$. We can substitute $\sec^2 x$:
$$ 1 + \tan^2 x = -2 \cot x $$
This can also be expressed as:
$$ 1 + \tan^2 x = -2 \frac{1}{\tan x} $$
- Multiplying through by $\tan x$
To eliminate the fraction, multiply both sides by $\tan x$ (assuming $\tan x \neq 0$):
$$ \tan x + \tan^3 x = -2 $$
- Rearranging to form a polynomial
This gives us the polynomial equation:
$$ \tan^3 x + \tan x + 2 = 0 $$
- Substituting $y = \tan x$
Let $y = \tan x$:
$$ y^3 + y + 2 = 0 $$
- Using the Rational Root Theorem
To find rational roots, we can test possible values. Testing $y = -1$:
$$ (-1)^3 + (-1) + 2 = -1 - 1 + 2 = 0 $$
Thus, $y = -1$ is a root.
- Factoring the polynomial
Now we can factor the polynomial using synthetic division or polynomial division. Dividing:
$$ y^3 + y + 2 = (y + 1)(y^2 - y + 2) $$
- Solving for the remaining roots
Next, we solve $y^2 - y + 2 = 0$ using the quadratic formula:
$$ y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{1 \pm \sqrt{1 - 8}}{2} = \frac{1 \pm \sqrt{-7}}{2} $$
This yields complex roots. We focus on:
$$ y = \tan x = -1 $$
- Finding the angles for $\tan x = -1$
The angles where $\tan x = -1$ are $x = \frac{3\pi}{4} + n\pi$, where $n$ is any integer.
The solution is:
$$ x = \frac{3\pi}{4} + n\pi $$
where $n \in \mathbb{Z}$.
More Information
The equation was solved using trigonometric identities and factoring techniques. Recognizing that $\tan x = -1$ leads to angles in specific quadrants is crucial when solving trigonometric equations.
Tips
- Not using the correct trigonometric identities, which can lead to wrong simplifications.
- Forgetting to check for both real and complex roots when solving polynomial equations.
AI-generated content may contain errors. Please verify critical information