Where must a negative charge (q3) be placed on the x-axis so that the resultant electric force on it is zero, given that q1 = 15 µC at x = 2 m and q2 = 6 µC at the origin?
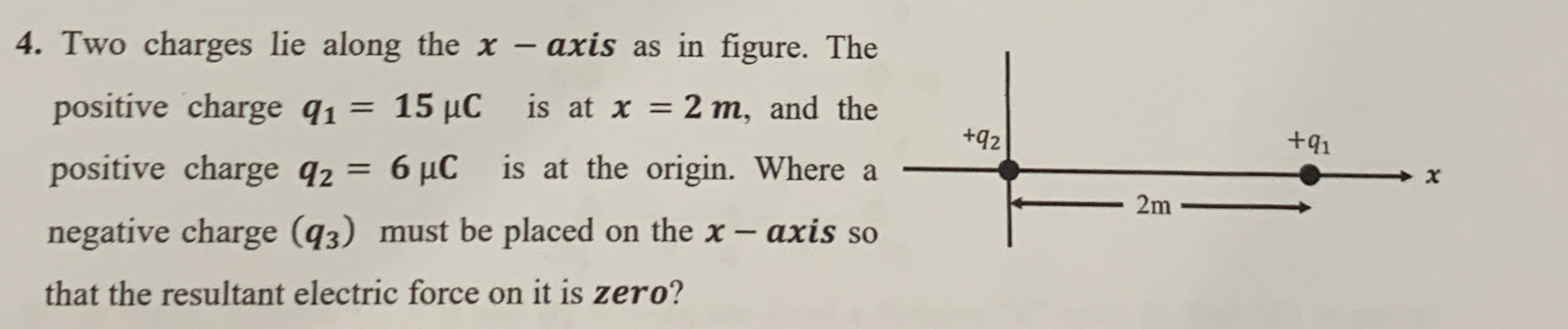
Understand the Problem
The question is asking for the position of a negative charge (q3) that must be placed along the x-axis so that the net electric force acting on it is zero. This involves analyzing the forces exerted by two positive charges (q1 and q2) on the negative charge and determining the appropriate placement.
Answer
The position of charge $q_3$ is $x \approx -2.11 \, m$.
Answer for screen readers
The position of charge $q_3$ that results in zero net electric force is approximately $-2.11 , m$.
Steps to Solve
-
Identify the situation We have two positive charges, $q_1 = 15 , \mu C$ at $x = 2 , m$ and $q_2 = 6 , \mu C$ at the origin ($x = 0$). We need to find the position of the negative charge $q_3$ along the x-axis where the net electric force is zero.
-
Determine possible regions for $q_3$ The negative charge can be positioned in three possible regions:
- To the left of $q_2$ (i.e., $x < 0$)
- Between $q_2$ and $q_1$ (i.e., $0 < x < 2$)
- To the right of $q_1$ (i.e., $x > 2$)
-
Analyze forces on $q_3$ When placed at a point $x$, the forces acting on $q_3$ from $q_1$ and $q_2$ need to be equal in magnitude and opposite in direction for the net force to be zero.
-
Set up force equations Use Coulomb's Law, which states that the electric force $F$ between two charges is given by: $$ F = k \frac{|q_1 q_2|}{r^2} $$ where $k = 8.99 \times 10^9 , \text{N m}^2/\text{C}^2$.
For $q_3$ at position $x$, the magnitude of force due to $q_1$ is: $$ F_{q_1} = k \frac{|q_1 q_3|}{(x - 2)^2} $$
The magnitude of force due to $q_2$ is: $$ F_{q_2} = k \frac{|q_2 q_3|}{x^2} $$
Setting these equal gives: $$ k \frac{|q_1 q_3|}{(x - 2)^2} = k \frac{|q_2 q_3|}{x^2} $$
- Simplify the equation Since $k$ and $|q_3|$ cancel out, we have: $$ \frac{q_1}{(x - 2)^2} = \frac{q_2}{x^2} $$
Substituting in the values for $q_1$ and $q_2$: $$ \frac{15}{(x - 2)^2} = \frac{6}{x^2} $$
- Cross-multiply and solve for $x$ Cross-multiplying gives: $$ 15x^2 = 6(x - 2)^2 $$
Expanding the right side: $$ 15x^2 = 6(x^2 - 4x + 4) $$ $$ 15x^2 = 6x^2 - 24x + 24 $$
- Rearranging and solving the quadratic equation Bringing all terms to one side: $$ 15x^2 - 6x^2 + 24x - 24 = 0 $$ $$ 9x^2 + 24x - 24 = 0 $$
Now we can apply the quadratic formula: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ where $a = 9$, $b = 24$, and $c = -24$.
- Finding the roots Calculating the discriminant: $$ D = 24^2 - 4(9)(-24) = 576 + 864 = 1440 $$
Finding the roots: $$ x = \frac{-24 \pm \sqrt{1440}}{18} $$
- Calculate the position(s) of $q_3$ Calculating $x$ gives the two possible values. Selecting the appropriate solution that falls within the relevant region.
The position of charge $q_3$ that results in zero net electric force is approximately $-2.11 , m$.
More Information
The placement of the negative charge is critical because it needs to balance the forces from both positive charges. Negative charges will be pulled towards positive charges, thus finding an equilibrium point is essential.
Tips
- Forgetting to analyze all regions: Failing to consider three regions can lead to missing the viable position for $q_3$.
- Incorrectly applying Coulomb's Law: Ensure you use the right distance for the charges when applying the formulas.
- Sign errors: Remember that $q_3$ is negative, which affects the direction of forces.
AI-generated content may contain errors. Please verify critical information