What are the properties or calculations related to the geometrical figure with dimensions labeled as 2a and 6a?
Understand the Problem
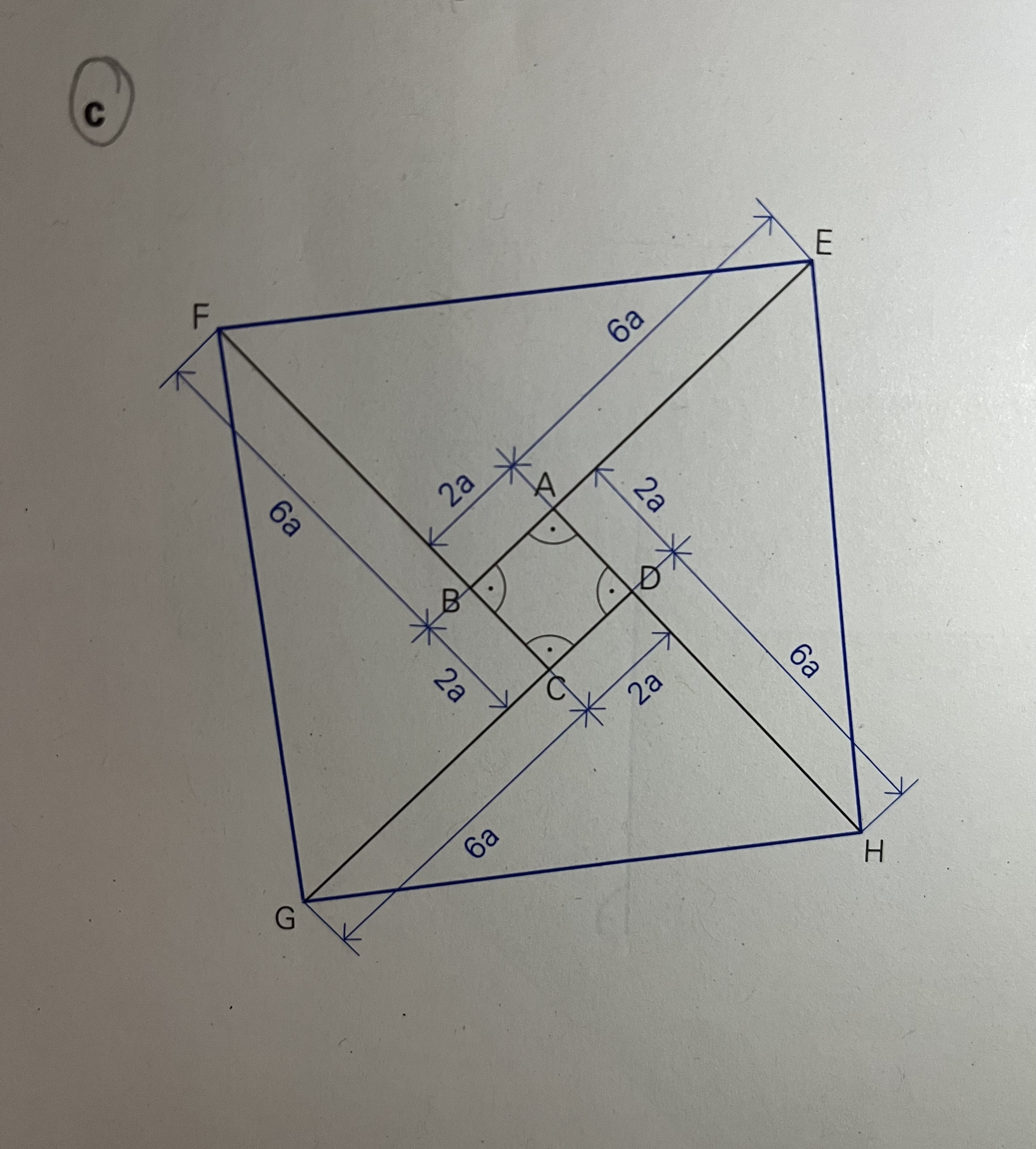
The question involves a geometric figure with marked dimensions. It likely asks for calculations or properties related to the figure, such as finding the area, perimeter, angles, or relationships among the segments based on the given dimensions.
Answer
The remaining area is given by $$ 18\sqrt{3} a^2 - 4a^2 $$.
Answer for screen readers
The remaining area of the figure is: $$ 18\sqrt{3} a^2 - 4a^2 $$
Steps to Solve
-
Identify Dimensions and Layout Begin by identifying the marked dimensions in the figure. The outer shape is a rhombus with each side measuring $6a$. The inner square, denoted by points A, B, C, D, has its sides measuring $2a$.
-
Calculate the Area of the Rhombus The area of a rhombus can be calculated using the formula: $$ \text{Area}_{\text{rhombus}} = \frac{1}{2} \times d_1 \times d_2 $$ where $d_1$ and $d_2$ are the diagonals. The diagonals can be determined by $d_1 = 2(6a) = 12a$ and $d_2 = 2(6a) = 12a$ based on the arrangement.
-
Calculate the Area of the Inner Square The area of the inner square is: $$ \text{Area}_{\text{square}} = s^2 = (2a)^2 = 4a^2 $$
-
Determine the Area of the Rhombus Using Sides and Height Another way to calculate the area of the rhombus is by using the height. The height can be derived from the Pythagorean theorem: $$ h = \sqrt{(6a)^2 - (3a)^2} = \sqrt{36a^2 - 9a^2} = \sqrt{27a^2} = 3\sqrt{3} a $$ Thus, $$ \text{Area}_{\text{rhombus}} = \text{base} \times \text{height} = 6a \times 3\sqrt{3} a = 18\sqrt{3} a^2 $$
-
Compute the Remaining Area To find the area outside the inner square, subtract the area of the square from the area of the rhombus: $$ \text{Remaining Area} = \text{Area}{\text{rhombus}} - \text{Area}{\text{square}} $$ Putting in the values: $$ \text{Remaining Area} = 18\sqrt{3} a^2 - 4a^2 $$
The remaining area of the figure is: $$ 18\sqrt{3} a^2 - 4a^2 $$
More Information
The structure is a complex geometric arrangement that involves both rhombus and square calculations. Understanding the relationships between diagonals, sides, and areas is crucial in geometry, especially in composite shapes.
Tips
- Forgetting to calculate the height of the rhombus correctly, leading to an incorrect area.
- Mixing up the dimensions of the rectangular/square area being subtracted from the area of the rhombus.
- Not using the correct formulas for area calculations when dealing with composite shapes.
AI-generated content may contain errors. Please verify critical information