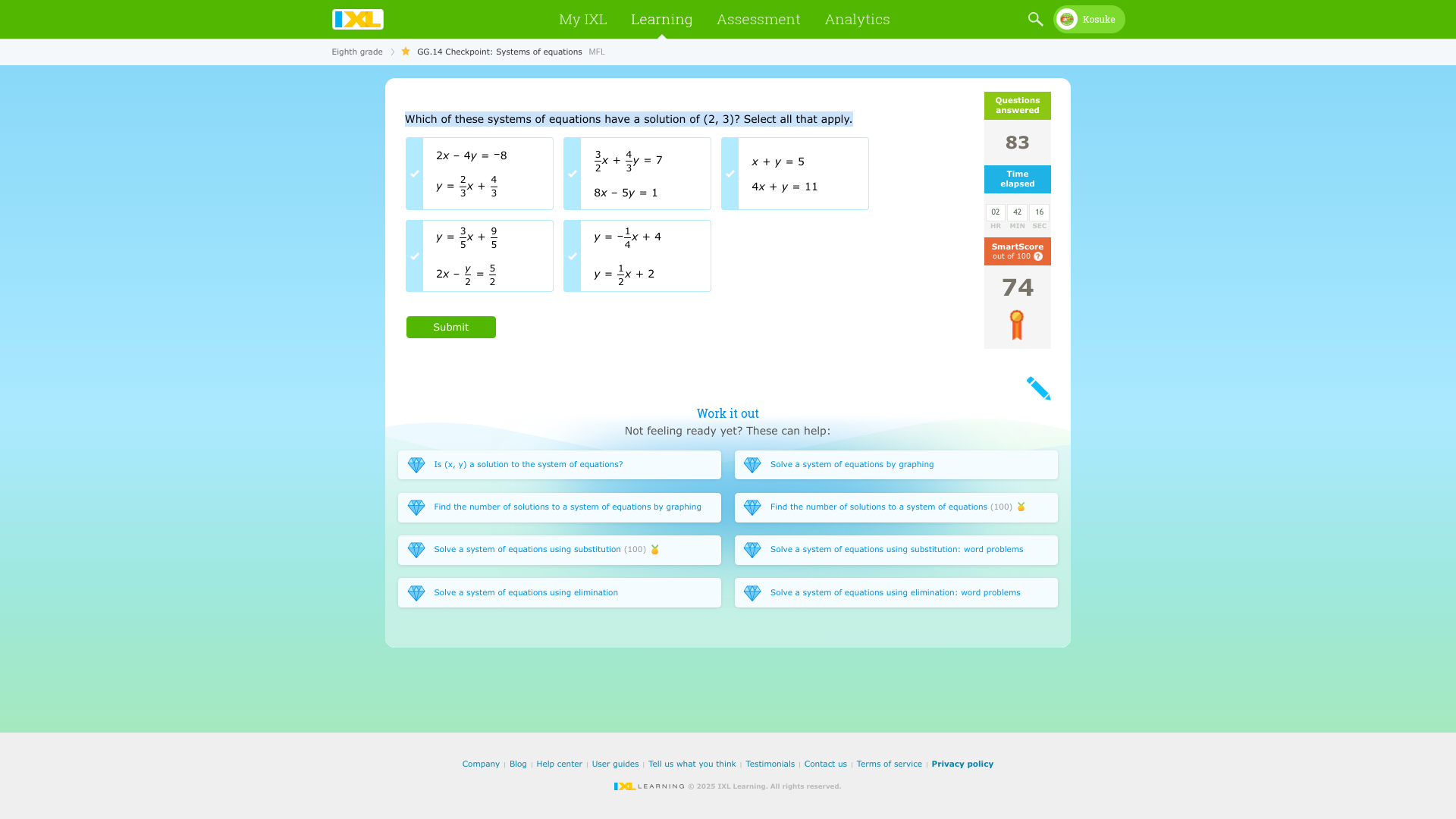
Which of these systems of equations have a solution of (2, 3)? Select all that apply.

Steps to Solve

1. Identify the system of equations to test We need to check each of the equations listed to see if they hold true when $x = 2$ and $y = 3$.

2. Substitute values into the first system For the first system: $$2x - 4y = -8$$ Substitute $x = 2$ and $y = 3$: $$2(2) - 4(3) = -8$$ Calculate: $$4 - 12 = -8$$ This is true.

3. Substitute values into the second system For the second system: $$y = \frac{2}{3}x + \frac{4}{3}$$ Substitute $x = 2$: $$y = \frac{2}{3}(2) + \frac{4}{3} = \frac{4}{3} + \frac{4}{3} = \frac{8}{3}$$ Since $y$ should equal 3, this is false.

4. Substitute values into the third system For the third system: $$\frac{3}{5}x + \frac{4}{3}y = 7$$ Substitute $x = 2$ and $y = 3$: $$\frac{3}{5}(2) + \frac{4}{3}(3) = \frac{6}{5} + 4 = \frac{6}{5} + \frac{20}{5} = \frac{26}{5}$$ Since $7$ is equivalent to $\frac{35}{5}$, this is false.

5. Substitute values into the fourth system For the fourth system: $$8x - 5y = 1$$ Substitute $x = 2$ and $y = 3$: $$8(2) - 5(3) = 16 - 15 = 1$$ This is true.

6. Continue testing remaining systems Repeat the substitution process for the last two systems:

   • For: $$x + y = 5$$ → $2 + 3 = 5$ (true).
   • For: $$4x + y = 11$$ → $4(2) + 3 = 8 + 3 = 11$ (true).

7. List all systems that are true The systems that have a solution of $(2, 3)$ are:

   • $2x - 4y = -8$
   • $8x - 5y = 1$
   • $x + y = 5$
   • $4x + y = 11$