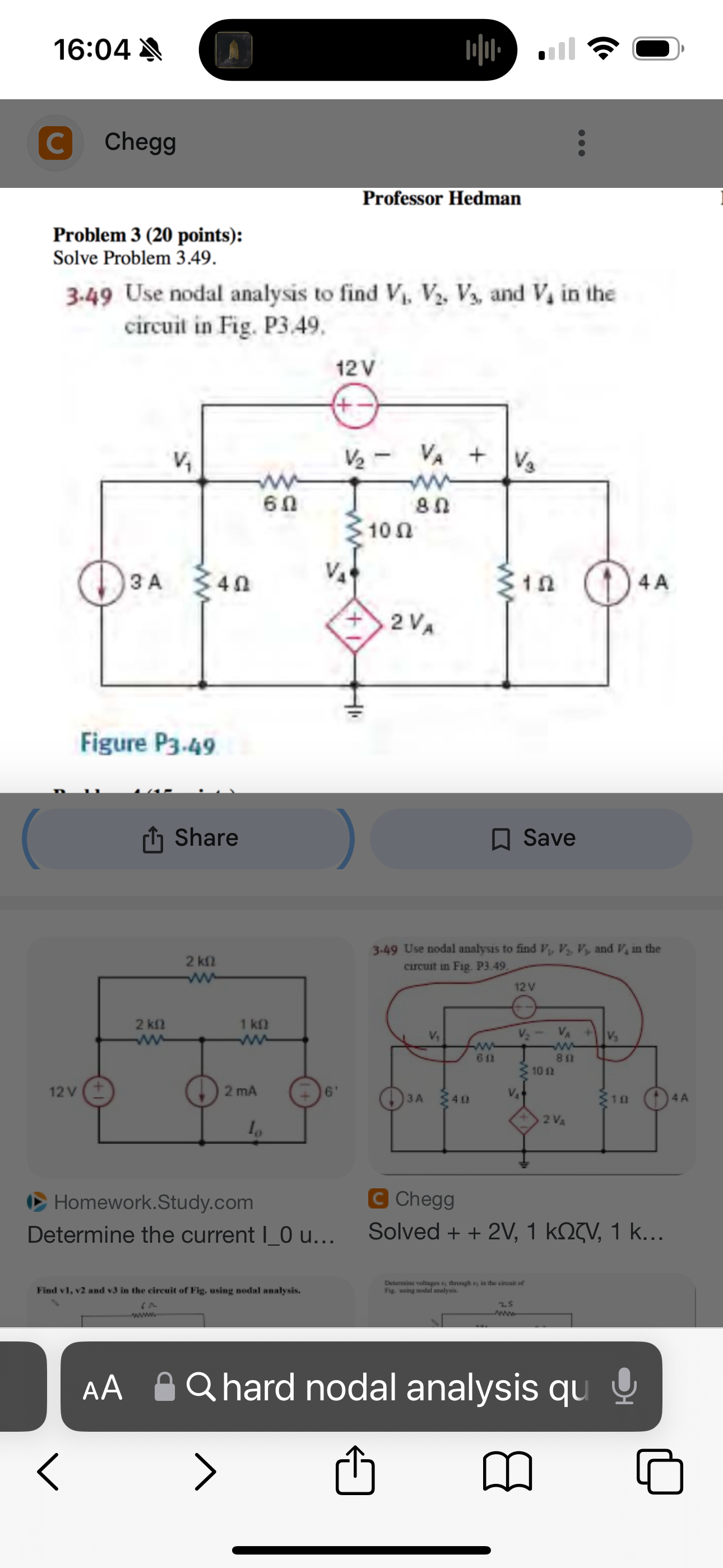
Use nodal analysis to find V1, V2, V3, and V4 in the circuit in Fig. P3.49.

Steps to Solve

1. Identify Nodes and Reference Node

Label the nodes in the circuit: V1 at the top left, V2 at the top right, V3 at the middle, and V4 at the bottom middle. Choose the bottom node as the reference (ground) where the voltage is 0V.

2. Apply KCL at Node V1

Using Kirchhoff's Current Law (KCL), sum the currents leaving Node V1. The equation is: $$ \frac{V1 - 12}{4} + \frac{V1 - V2}{6} + 3 = 0 $$

3. Apply KCL at Node V2

For Node V2, apply KCL to find the currents: $$ \frac{V2 - V1}{6} + \frac{V2 - V3}{8} - \frac{V4}{10} = 0 $$

4. Apply KCL at Node V3

At Node V3, the KCL equation is: $$ \frac{V3 - V2}{8} + \frac{V3 - V4}{10} - 4 = 0 $$

5. Apply KCL at Node V4

For Node V4 with the dependent source (2VA): $$ \frac{V4 - V1}{4} + \frac{V4 - 2V4}{10} + \frac{V4}{2} = 0 $$ This simplifies to: $$ \frac{V4 - V1}{4} - \frac{V4}{10} = 0 $$

6. Set Up the System of Equations

You'll have four equations from the above steps:

1. From V1: ( \frac{V1 - 12}{4} + \frac{V1 - V2}{6} + 3 = 0 )

2. From V2: ( \frac{V2 - V1}{6} + \frac{V2 - V3}{8} - \frac{V4}{10} = 0 )

3. From V3: ( \frac{V3 - V2}{8} + \frac{V3 - V4}{10} - 4 = 0 )

4. From V4: ( \frac{V4 - V1}{4} - \frac{V4}{10} = 0 )

5. Solve the System of Equations

Use substitution or matrix methods to solve for V1, V2, V3, and V4.