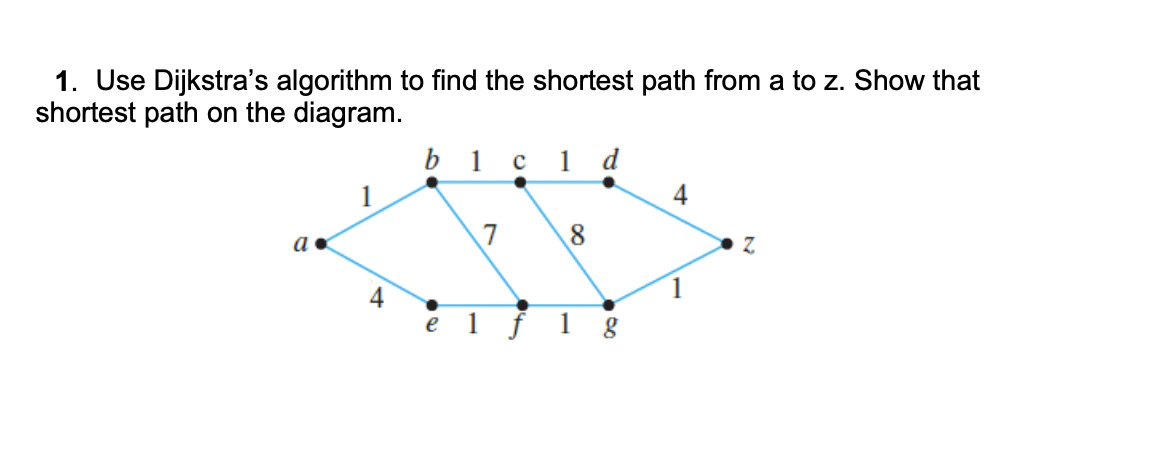
Use Dijkstra's algorithm to find the shortest path from a to z. Show that shortest path on the diagram.
Understand the Problem
The question is asking to apply Dijkstra's algorithm to find the shortest path from point 'a' to point 'z' in the given diagram and illustrate that path on the diagram.
Answer
The shortest path from 'a' to 'z' is $a \rightarrow b \rightarrow f \rightarrow z$ with a distance of 6.
Answer for screen readers
The shortest path from 'a' to 'z' is represented by the path $a \rightarrow b \rightarrow f \rightarrow z$ with a total distance of 6.
Steps to Solve
- Initialization
Start by initializing the distances from point 'a' to all other points. Set the distance to 'a' as 0 and all others as infinity.
$$ \text{Distance}(a) = 0, \quad \text{Distance}(b) = \infty, \quad \text{Distance}(c) = \infty, \quad \text{Distance}(d) = \infty, \quad \text{Distance}(e) = \infty, \quad \text{Distance}(f) = \infty, \quad \text{Distance}(g) = \infty, \quad \text{Distance}(z) = \infty $$
- Choose the Minimum Distance Node
Select the node with the smallest distance value, which is 'a' (distance 0). Mark 'a' as visited.
- Update Neighbor Distances
Update the distances to the neighboring nodes of 'a':
- For 'b': Distance = 0 + 1 = 1
- For 'e': Distance = 0 + 4 = 4
New distances: $$ \text{Distance}(b) = 1, \quad \text{Distance}(e) = 4 $$
- Next Minimum Distance Node
Choose the next node with the smallest distance, which is 'b' (distance 1) and mark it visited.
- Update Neighbor Distances from 'b'
Update the distances to the neighbors of 'b':
- For 'c': Distance = 1 + 1 = 2
- For 'g': Distance = 1 + 8 = 9
New distances: $$ \text{Distance}(c) = 2, \quad \text{Distance}(g) = 9 $$
- Continue to Next Node
Next, select 'c' (distance 2) and mark it visited. From 'c', update distances:
- For 'd': Distance = 2 + 7 = 9
New distances: $$ \text{Distance}(d) = 9 $$
- Choose 'e' Next
Select 'e' (distance 4), update:
- For 'f': Distance = 4 + 1 = 5
New distances: $$ \text{Distance}(f) = 5 $$
- Continue with 'f'
Move to 'f' (distance 5) and update:
- For 'g': Distance = 5 + 1 = 6
- For 'z': Distance = 5 + 1 = 6
New distances: $$ \text{Distance}(z) = 6 $$
- Final Steps
Continue with remaining nodes, updating as follows:
- For 'd' (distance now 9) and finally 'g' (6).
The shortest path is found with distances: $$ \text{Distance}(z) = 6 \quad \text{via path } a \rightarrow b \rightarrow f \rightarrow z $$
- Conclusion
Mark the shortest path on the diagram as 'a → b → f → z'.
The shortest path from 'a' to 'z' is represented by the path $a \rightarrow b \rightarrow f \rightarrow z$ with a total distance of 6.
More Information
Dijkstra's algorithm efficiently finds the shortest path in a weighted graph by systematically exploring nodes and updating their distances based on the edges' weights. The algorithm ensures that the shortest paths to all nodes are found by continuously selecting the closest unvisited node.
Tips
- Overlooking Edge Weights: Always ensure that the weights of edges are accurately considered when updating distances.
- Not Marking Nodes Visited: Failing to mark nodes as visited may cause incorrect calculations as nodes can be revisited.
AI-generated content may contain errors. Please verify critical information