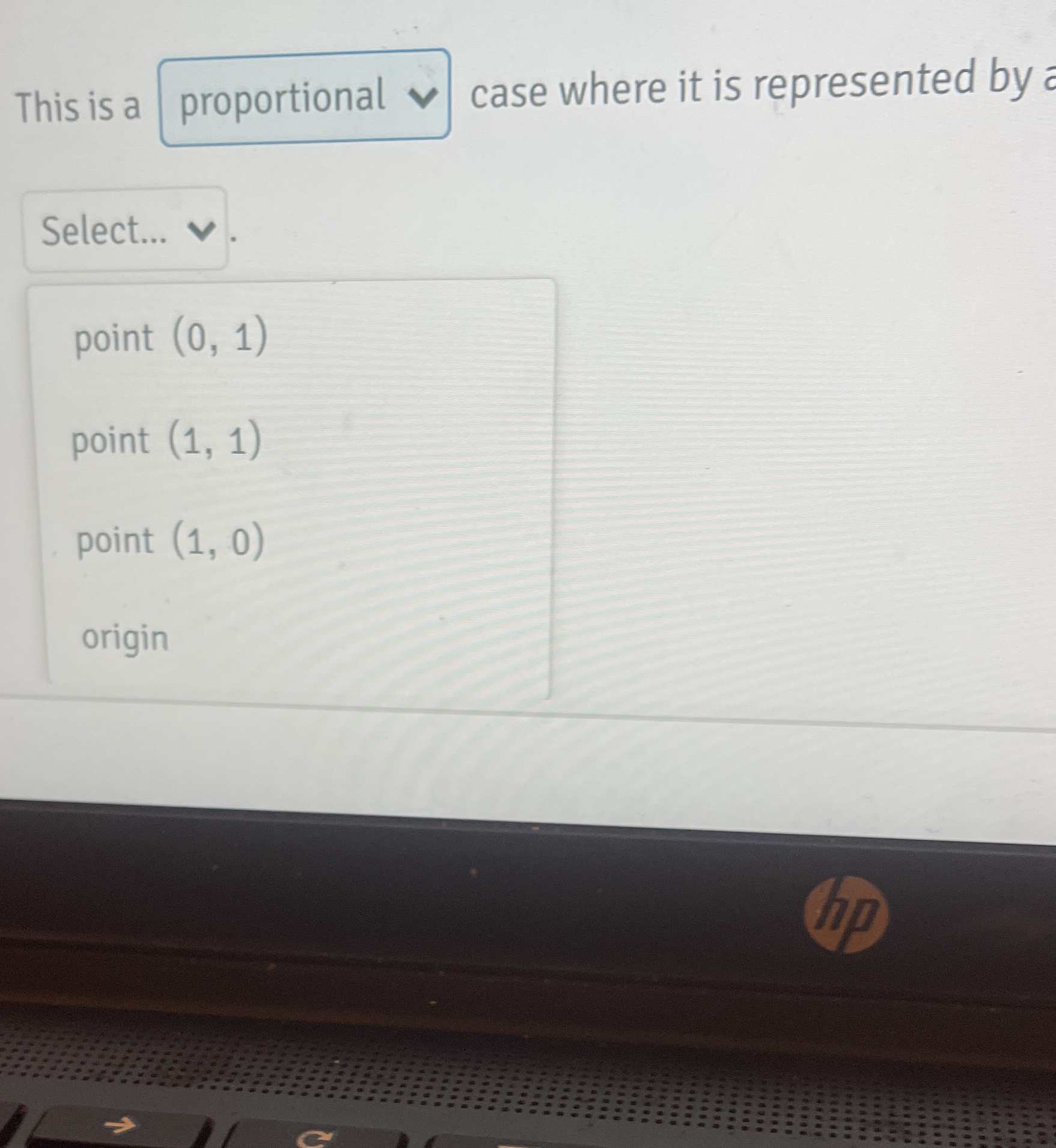
This is a proportional case where it is represented by a Select...
Understand the Problem
The question appears to ask for a selection of a specific point that illustrates a proportional case in a mathematical context, likely related to coordinate systems or graphing. The option choices suggest different points that could represent this proportional relationship.
Answer
The proportional point is $(1, 1)$.
Answer for screen readers
The point that represents a proportional case is the point $(1, 1)$.
Steps to Solve
-
Understanding Proportional Relationships Proportional relationships can be defined as those in which two quantities always have the same ratio. This means if you have a proportional relationship expressed as $y = kx$, for some constant $k$, the graph will be a straight line that passes through the origin.
-
Identifying Points in the Options We need to evaluate the given points:
- Point (0, 1)
- Point (1, 1)
- Point (1, 0)
- Origin (0, 0)
- Checking Each Point for Proportionality
- Point (0, 1): This point does not pass through the origin, thus it represents a non-proportional relationship.
- Point (1, 1): Here, the ratio is $y/x = 1/1 = 1$. This is proportional.
- Point (1, 0): This point also does not pass through the origin, making it non-proportional.
- Origin (0, 0): This point clearly represents a proportional relationship as every line through the origin is proportional.
- Conclusion on Proportional Points The point (1, 1) is the best representative of a proportional case from the options given, as it maintains the property of a constant ratio.
The point that represents a proportional case is the point $(1, 1)$.
More Information
In a proportional relationship, if one value increases, the other must increase at the same rate, hence maintaining a constant ratio. The line representing this relationship is always a straight line passing through the origin.
Tips
Common mistakes include:
- Confusing points that do not pass through the origin as proportional.
- Misunderstanding that any straight line can be proportional, while only those through the origin and maintaining a constant ratio are.
AI-generated content may contain errors. Please verify critical information