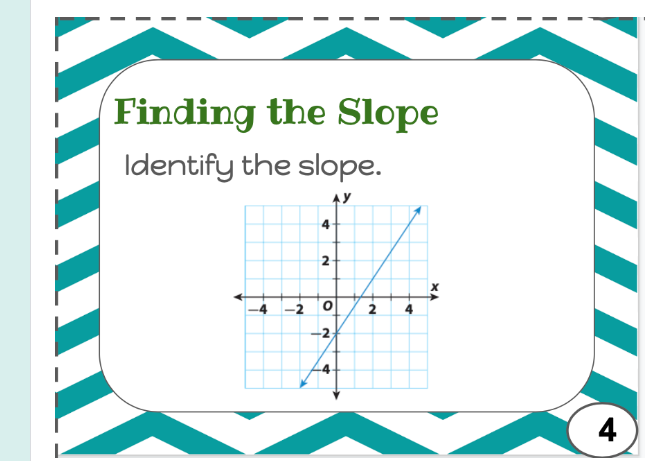
Identify the slope.
Understand the Problem
The question is asking us to identify the slope of a line shown in a graph. To solve this, we need to determine the rise over run of the line represented on the Cartesian plane.
Answer
The slope of the line is \( m = 1 \).
Answer for screen readers
The slope of the line is ( m = 1 ).
Steps to Solve
- Identify two points on the line
Locate two points that the line passes through. For example, let's choose the points $(0, 1)$ and $(2, 3)$.
- Calculate the rise
The rise is calculated by taking the difference in the $y$-coordinates of the two points.
Using the points $(0, 1)$ and $(2, 3)$, the rise is:
$$ \text{Rise} = y_2 - y_1 = 3 - 1 = 2 $$
- Calculate the run
The run is calculated by taking the difference in the $x$-coordinates of the two points.
Using the points $(0, 1)$ and $(2, 3)$, the run is:
$$ \text{Run} = x_2 - x_1 = 2 - 0 = 2 $$
- Calculate the slope
The slope ($m$) of the line can be calculated using the formula:
$$ m = \frac{\text{Rise}}{\text{Run}} $$
Substituting the values we found:
$$ m = \frac{2}{2} = 1 $$
The slope of the line is ( m = 1 ).
More Information
The slope of a line represents its steepness and direction. A slope of ( 1 ) means that for every one unit the line rises vertically, it moves one unit horizontally, leading to a 45-degree angle.
Tips
- Confusing rise with run: Always remember to order the coordinates correctly when subtracting.
- Selecting points that are not easily identifiable or do not lie on the line, which could lead to incorrect calculations.
AI-generated content may contain errors. Please verify critical information