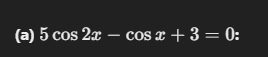
5 cos 2x - cos x + 3 = 0

Steps to Solve

1. Use the double angle identity for cosine

The double angle identity states that $\cos(2x) = 2\cos^2(x) - 1$. We'll use this to rewrite the equation.

Substituting this into the equation, we have:

$$ 5(2\cos^2(x) - 1) - \cos(x) + 3 = 0 $$

2. Simplify the equation

Distributing and combining like terms:

$$ 10\cos^2(x) - 5 - \cos(x) + 3 = 0 $$

This simplifies to:

$$ 10\cos^2(x) - \cos(x) - 2 = 0 $$

3. Rewrite as a quadratic equation

We can rearrange the expression into a standard form for a quadratic equation:

$$ 10\cos^2(x) - \cos(x) - 2 = 0 $$

This is a quadratic in terms of $\cos(x)$.

4. Use the quadratic formula

Now, we will use the quadratic formula, $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, with $a = 10$, $b = -1$, and $c = -2$:

First, we calculate the discriminant:

$$ D = b^2 - 4ac = (-1)^2 - 4(10)(-2) = 1 + 80 = 81 $$

Now plug values into the quadratic formula:

$$ \cos(x) = \frac{-(-1) \pm \sqrt{81}}{2(10)} = \frac{1 \pm 9}{20} $$

5. Calculate the possible values for $\cos(x)$

From the quadratic formula, we get two solutions for $\cos(x)$:

1. For the positive case:

$$ \cos(x) = \frac{1 + 9}{20} = \frac{10}{20} = \frac{1}{2} $$

2. For the negative case:

$$ \cos(x) = \frac{1 - 9}{20} = \frac{-8}{20} = -\frac{2}{5} $$

6. Solve for angles x

For $\cos(x) = \frac{1}{2}$, the solutions are:

$$ x = \frac{\pi}{3} + 2k\pi \text{ or } x = -\frac{\pi}{3} + 2k\pi \quad (k \in \mathbb{Z}) $$

For $\cos(x) = -\frac{2}{5}$, use the inverse cosine:

$$ x = \cos^{-1}\left(-\frac{2}{5}\right) + 2k\pi \quad \text{or} \quad x = -\cos^{-1}\left(-\frac{2}{5}\right) + 2k\pi \quad (k \in \mathbb{Z}) $$