sin(π/4 + x) + sin(π/4 - x) = √2 cos x
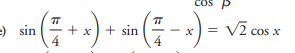
Understand the Problem
The question involves an equation with trigonometric functions that needs to be solved. We will need to apply trigonometric identities and possibly some algebraic manipulation to address the given expression.
Answer
The equation is true for all \( x \).
Answer for screen readers
The equation is true for all ( x ).
Steps to Solve
-
Apply the Sum-to-Product Identity To simplify the left side, we can use the sum-to-product identities for sine: $$ \sin(a + b) + \sin(a - b) = 2 \sin(a) \cos(b) $$ Here, let ( a = \frac{\pi}{4} ) and ( b = x ). Thus, we get: $$ \sin\left(\frac{\pi}{4} + x\right) + \sin\left(\frac{\pi}{4} - x\right) = 2 \sin\left(\frac{\pi}{4}\right) \cos(x) $$
-
Substituting the Known Values We know that ( \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} ). Substituting this in: $$ 2 \sin\left(\frac{\pi}{4}\right) \cos(x) = 2 \cdot \frac{\sqrt{2}}{2} \cos(x) = \sqrt{2} \cos(x) $$
-
Equating Both Sides Now we have: $$ \sqrt{2} \cos(x) = \sqrt{2} \cos(x) $$
-
Conclusion This equation is true for all values of ( x ) where ( \cos(x) ) is defined, meaning the original equation holds true for any ( x ).
The equation is true for all ( x ).
More Information
The identity we used shows that the original equation is valid universally, highlighting the periodic nature of trigonometric functions. This reinforces the importance of understanding trigonometric identities in simplifying expressions.
Tips
- Failing to apply the sum-to-product identities correctly.
- Not substituting the values for sine and cosine.
AI-generated content may contain errors. Please verify critical information