Prove that: (A ∪ B) ∩ C = A ∩ (B ∩ C)
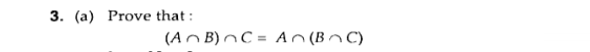
Understand the Problem
The question is asking to prove a set theory equation involving the intersection and union of sets A, B, and C. This involves demonstrating that (A ∪ B) ∩ C is equal to A ∩ (B ∩ C).
Answer
$$(A \cup B) \cap C = A \cap (B \cap C)$$
Answer for screen readers
$$(A \cup B) \cap C = A \cap (B \cap C)$$
Steps to Solve
-
Recall Set Definitions To prove the equation, we need to understand the definitions of union ($\cup$) and intersection ($\cap$) in set theory.
- Union ($A \cup B$): The set containing all elements from both $A$ and $B$.
- Intersection ($A \cap B$): The set containing elements that are in both $A$ and $B$.
-
Rewrite the Left Side Start with the left side of the equation: $$(A \cup B) \cap C$$ This means we are interested in elements that are both in the union of $A$ and $B$, and also in set $C$.
-
Expand the Left Side Using Element Membership An element $x$ belongs to $(A \cup B) \cap C$ if:
- $x \in (A \cup B)$, meaning $x \in A$ or $x \in B$, and
- $x \in C$.
-
Analyze Membership in Component Sets Therefore, we can say:
- If $x \in (A \cup B) \cap C$, then $x \in C$ and either $x \in A$ or $x \in B$. This leads to two cases:
- Case 1: If $x \in A$, then $x \in (B \cap C)$.
- Case 2: If $x \in B$, then $x \in (C)$.
-
Focus on the Right Side Now consider the right side of the equation: $$A \cap (B \cap C)$$ This means we are looking for elements that are in both $A$ and the intersection of $B$ and $C$.
-
Expand the Right Side Using Element Membership For $x$ to belong to $A \cap (B \cap C)$, it must satisfy:
- $x \in A$ and $x \in B \cap C$, implying $x \in B$ and $x \in C$.
-
Show Both Sides Contain the Same Elements To show that $(A \cup B) \cap C = A \cap (B \cap C)$, we must prove that:
- If $x \in (A \cup B) \cap C$, then $x \in A \cap (B \cap C)$, and vice versa.
-
Final Conclusion Since both expressions represent the same logical conditions for elements, we conclude that: $$(A \cup B) \cap C = A \cap (B \cap C)$$
$$(A \cup B) \cap C = A \cap (B \cap C)$$
More Information
This equality is known as the "distribution of intersection over union" in set theory. It helps establish the relationships between sets and is foundational in understanding the properties of unions and intersections.
Tips
- Misunderstanding Basic Definitions: It's crucial to remember the definitions of union and intersection. Confusing them can lead to incorrect conclusions.
- Logical Errors: Failing to address both directions of the proof (i.e., showing both inclusions) can result in incomplete arguments.
AI-generated content may contain errors. Please verify critical information