In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.
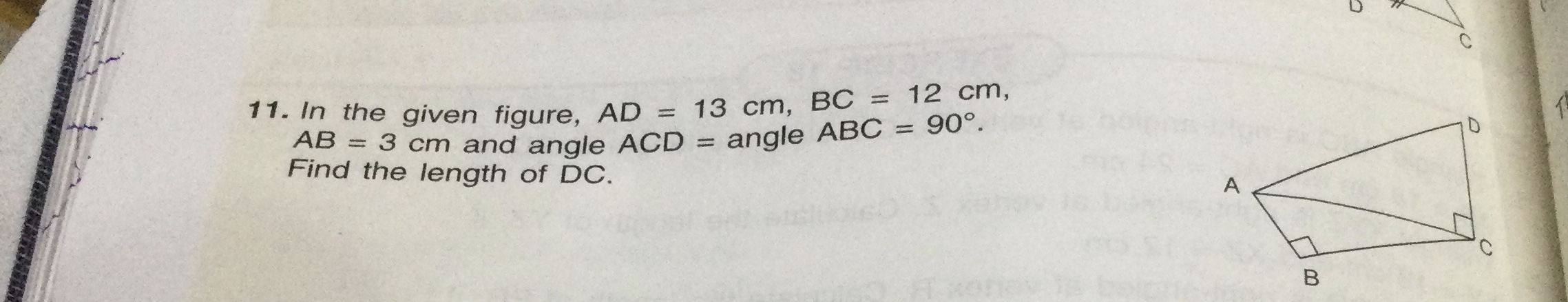
Understand the Problem
The question is asking to find the length of DC in a geometric figure. Given lengths and angles, we will apply the properties of right triangles to solve for the unknown side.
Answer
The length of DC is $4 \, \text{cm}$.
Answer for screen readers
The length of DC is $4 , \text{cm}$.
Steps to Solve
- Understanding the Right Triangle Properties
Given that angles ACD and ABC are both 90°, triangles ABC and ADC are right triangles. We can apply the Pythagorean theorem to find the unknown length DC.
- Applying the Pythagorean Theorem to Triangle ABC
In right triangle ABC, we know:
- ( AB = 3 , \text{cm} )
- ( BC = 12 , \text{cm} )
We can find AC using the Pythagorean theorem: $$ AC^2 = AB^2 + BC^2 $$
Substituting the values: $$ AC^2 = 3^2 + 12^2 $$
Calculating: $$ AC^2 = 9 + 144 = 153 $$ $$ AC = \sqrt{153} \approx 12.37 , \text{cm} $$
- Applying the Pythagorean Theorem to Triangle ACD
Now we can find DC. In triangle ACD:
- ( AD = 13 , \text{cm} )
- ( AC = \sqrt{153} )
Again we use the Pythagorean theorem: $$ AD^2 = AC^2 + DC^2 $$
Substituting the known values: $$ 13^2 = 153 + DC^2 $$
Calculating: $$ 169 = 153 + DC^2 $$ $$ DC^2 = 169 - 153 $$ $$ DC^2 = 16 $$ $$ DC = \sqrt{16} = 4 , \text{cm} $$
The length of DC is $4 , \text{cm}$.
More Information
In this problem, we utilized the properties of right triangles and the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Tips
- Misapplying the Pythagorean theorem by mixing up sides.
- Forgetting to square the components before summing them.
AI-generated content may contain errors. Please verify critical information