Graph the following function on the axes provided: f(x) = -4 for x ≤ 2; -x for x > 5.
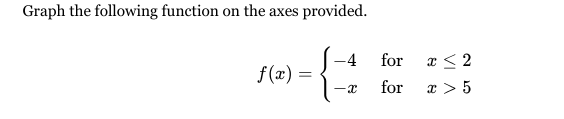
Understand the Problem
The question is asking to graph a piecewise function defined for two intervals: for x less than or equal to 2, f(x) equals -4, and for x greater than 5, f(x) equals -x. We need to visualize these segments on a graph.
Answer
The graph includes a horizontal line at $y = -4$ for $x \leq 2$ and a line with slope -1 starting from an open circle at (5, -5) for $x > 5$.
Answer for screen readers
The graph represents the function $f(x) = \begin{cases} -4 & \text{for } x \leq 2 \ -x & \text{for } x > 5 \end{cases}$ with a horizontal line at $y = -4$ (closed at $x=2$) and a downward sloping line starting at an open circle at (5, -5).
Steps to Solve
-
Identify the intervals of the piecewise function The function is defined in two pieces. For $x \leq 2$, $f(x) = -4$. For $x > 5$, $f(x) = -x$.
-
Graph the first piece ($x \leq 2$) For $x \leq 2$, draw a horizontal line at $y = -4$. This line continues from $x = -\infty$ to $x = 2$. At $x = 2$, it will be a filled circle since it includes the point.
-
Graph the second piece ($x > 5$) For this part, the function is $f(x) = -x$. This is a straight line with a slope of -1. Calculate the points starting from $x = 5$:
- At $x = 5$, $f(5) = -5$. This point is not included, so it will be an open circle at (5, -5).
- As $x$ increases, for example, at $x = 6$, $f(6) = -6$ (the point (6, -6) will be filled).
-
Draw the line for $f(x) = -x$ Continue drawing the line downward to the right. The line should go through points like (5, -5), (6, -6), and continues in that way as $x$ increases.
-
Summarize the graph You should now have a graph with a horizontal line at $y = -4$ until $x = 2$, and from $x = 5$ onward, a line moving downwards with a slope of -1.
The graph represents the function $f(x) = \begin{cases} -4 & \text{for } x \leq 2 \ -x & \text{for } x > 5 \end{cases}$ with a horizontal line at $y = -4$ (closed at $x=2$) and a downward sloping line starting at an open circle at (5, -5).
More Information
This piecewise function illustrates how different mathematical expressions can work together to define a single function over various regions of its domain. The horizontal line indicates a constant value, while the linear function shows a decreasing relationship for values beyond a certain point.
Tips
- Confusing the values at transition points. When sketching, ensure to represent the open and closed circles correctly.
- Forgetting to plot the second part of the function to the right of $x=5$.
AI-generated content may contain errors. Please verify critical information