What is the value of x in 9/7 - x = -2/3?

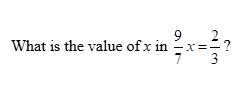
Understand the Problem

The question is asking to solve for the variable x in the equation $ \frac{9}{7} - x = -\frac{2}{3} $. This involves isolating x on one side of the equation.

Answer

The value of $ x $ is $ \frac{41}{21} $.

Steps to Solve

Rewrite the equation

Start with the original equation: $$ \frac{9}{7} - x = -\frac{2}{3} $$

Isolate x

To isolate ( x ), add ( x ) to both sides of the equation and then add ( -\frac{2}{3} ) to both sides: $$ \frac{9}{7} = x - \frac{2}{3} $$ $$ \frac{9}{7} + \frac{2}{3} = x $$

Find a common denominator

The least common multiple of 7 and 3 is 21. Convert both fractions: $$ \frac{9}{7} = \frac{9 \times 3}{7 \times 3} = \frac{27}{21} $$ $$ -\frac{2}{3} = \frac{-2 \times 7}{3 \times 7} = \frac{-14}{21} $$

Combine the fractions

Now substitute back into the equation: $$ x = \frac{27}{21} + \frac{14}{21} $$

Combine the numerators: $$ x = \frac{27 + 14}{21} = \frac{41}{21} $$

The value of ( x ) is ( \frac{41}{21} ).

More Information

The solution ( \frac{41}{21} ) is an improper fraction, which can also be represented as ( 1 \frac{20}{21} ). This fraction shows that ( x ) is slightly more than 1 and less than 2.

Tips

Not finding a common denominator: When adding fractions, forgetting to find a common denominator can lead to incorrect results.
Misplacing negative signs: Be cautious not to mix up signs during calculations, especially when isolating variables.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!