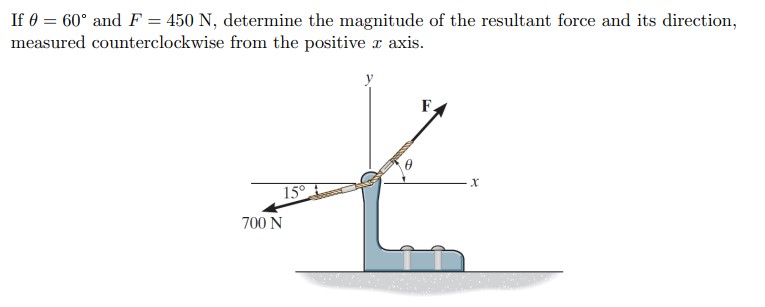
If θ = 60° and F = 450 N, determine the magnitude of the resultant force and its direction, measured counterclockwise from the positive x axis.

Steps to Solve

1. Determine the Components of Each Force

We need to break the forces into their x and y components.

For the first force ( F_1 = 450 , \text{N} ) at ( \theta_1 = 60^\circ ):

• ( F_{1x} = F_1 \cdot \cos(\theta_1) = 450 \cdot \cos(60^\circ) = 450 \cdot 0.5 = 225 , \text{N} )
• ( F_{1y} = F_1 \cdot \sin(\theta_1) = 450 \cdot \sin(60^\circ) = 450 \cdot \frac{\sqrt{3}}{2} \approx 389.74 , \text{N} )

For the second force ( F_2 = 700 , \text{N} ) at ( \theta_2 = 15^\circ ):

• ( F_{2x} = F_2 \cdot \cos(\theta_2) = 700 \cdot \cos(15^\circ) \approx 700 \cdot 0.9659 \approx 676.13 , \text{N} )
• ( F_{2y} = F_2 \cdot \sin(\theta_2) = 700 \cdot \sin(15^\circ) \approx 700 \cdot 0.2588 \approx 181.16 , \text{N} )

2. Sum the Components

Now we will sum the x and y components separately to find the resultant force components ( R_x ) and ( R_y ).

• Total x-component: $$ R_x = F_{1x} + F_{2x} = 225 + 676.13 \approx 901.13 , \text{N} $$

• Total y-component: $$ R_y = F_{1y} + F_{2y} = 389.74 + 181.16 \approx 570.90 , \text{N} $$

3. Calculate the Magnitude of the Resultant Force

The magnitude of the resultant force ( R ) can be found using the Pythagorean theorem: $$ R = \sqrt{R_x^2 + R_y^2} = \sqrt{(901.13)^2 + (570.90)^2} $$

Calculating: $$ R \approx \sqrt{812032.62 + 326126.81} \approx \sqrt{1139159.43} \approx 1067.17, \text{N} $$

4. Determine the Direction of the Resultant Force

The direction ( \theta_R ) can be calculated using the arctangent function: $$ \theta_R = \tan^{-1} \left( \frac{R_y}{R_x} \right) = \tan^{-1} \left( \frac{570.90}{901.13} \right) $$

Calculating: $$ \theta_R \approx \tan^{-1}(0.634) \approx 32.53^\circ $$

5. Final Result

Combine the magnitude and direction to summarize the resultant force.