∑ (from n=1 to 11) (3/4)^n
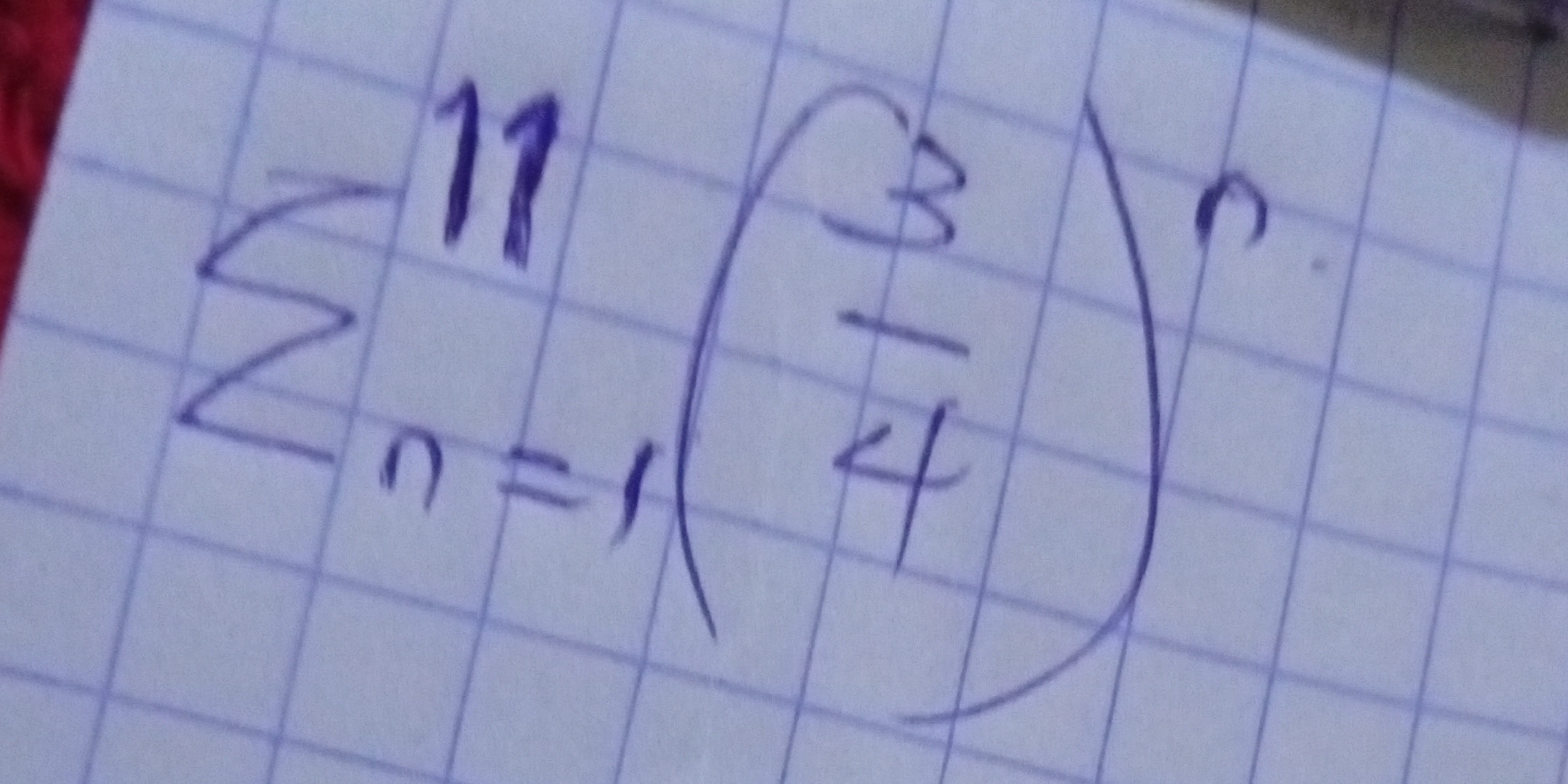
Understand the Problem
The question appears to be related to a mathematical summation that starts at n = 1 and ends at 11, indicating a series involving the fraction 3/4 raised to the power of n. It requires evaluating or simplifying this summation.
Answer
The sum is approximately \( S \approx 2.905 \).
Answer for screen readers
The final sum is approximately ( S \approx 2.905 ).
Steps to Solve
- Identify the summation formula
The summation can be expressed as:
$$ S = \sum_{n=1}^{11} \left(\frac{3}{4}\right)^n $$
- Use the formula for a geometric series
The sum of a geometric series can be calculated using the formula:
$$ S_n = a \frac{1 - r^n}{1 - r} $$
where:
- ( S_n ) is the sum of the series
- ( a ) is the first term
- ( r ) is the common ratio
- ( n ) is the number of terms
In this case, ( a = \frac{3}{4} ), ( r = \frac{3}{4} ), and ( n = 11 ).
- Substitute values into the formula
Now, substitute ( a ), ( r ), and ( n ) into the formula:
$$ S = \left(\frac{3}{4}\right) \frac{1 - \left(\frac{3}{4}\right)^{11}}{1 - \frac{3}{4}} $$
- Simplify the denominator
Calculate the denominator:
$$ 1 - \frac{3}{4} = \frac{1}{4} $$
- Substitute and simplify further
Replace the denominator in the sum:
$$ S = \left(\frac{3}{4}\right) \frac{1 - \left(\frac{3}{4}\right)^{11}}{\frac{1}{4}} $$
This simplifies to:
$$ S = 3 \left(1 - \left(\frac{3}{4}\right)^{11}\right) $$
- Calculate ( \left(\frac{3}{4}\right)^{11} )
Calculate ( \left(\frac{3}{4}\right)^{11} ):
Using a calculator,
$$ \left(\frac{3}{4}\right)^{11} \approx 0.031676352 $$
- Final substitution and computation
Now substitute back into the equation:
$$ S \approx 3 \left(1 - 0.031676352\right) \approx 3 (0.968323648) $$
This gives us:
$$ S \approx 2.904970944 $$
The final sum is approximately ( S \approx 2.905 ).
More Information
This sum is the evaluation of a finite geometric series, which allows for quick calculations without needing to add each term individually. The derived formula can be applied to many similar problems.
Tips
- Forgetting to use the correct formula for the geometric series.
- Miscalculating the powers, especially high exponents.
- Neglecting to simplify the fraction in the sum formula.
AI-generated content may contain errors. Please verify critical information