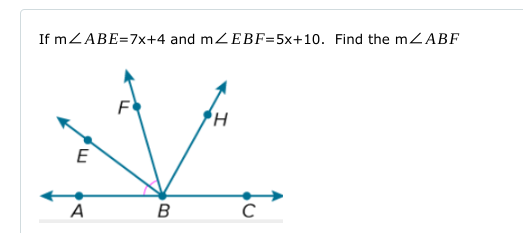
If m∠ABE=7x+4 and m∠EBF=5x+10. Find the m∠ABF.
Understand the Problem
The question is asking to find the measure of angle ABF, given the expressions for the measures of angles ABE and EBF in terms of x. Since angles ABE and EBF are adjacent and form a straight line, their measures can be added to equal 180 degrees. Therefore, we will set up the equation: (7x + 4) + (5x + 10) = 180 and solve for x to find the angle ABF.
Answer
$$m\angle ABF = \frac{475}{6} \text{ or } 79.17 \text{ degrees}$$
Answer for screen readers
$$m\angle ABF = \frac{475}{6} \text{ or } 79.17 \text{ degrees}$$
Steps to Solve
- Set Up the Equation
Since angles ABE and EBF are adjacent and form a straight line, we add them together to equal 180 degrees:
$$(7x + 4) + (5x + 10) = 180$$
- Combine Like Terms
Combine the expressions for $x$:
$$7x + 5x + 4 + 10 = 180$$
This simplifies to:
$$12x + 14 = 180$$
- Isolate x
To isolate $x$, subtract 14 from both sides:
$$12x = 180 - 14$$
This simplifies to:
$$12x = 166$$
- Solve for x
Divide both sides by 12:
$$x = \frac{166}{12} = \frac{83}{6}$$
- Substitute x Back to Find Angle ABF
Now substitute $x$ back into the expression for angle ABF, which is:
$$m\angle ABF = 5x + 10$$
Substituting in the value of $x$:
$$m\angle ABF = 5\left(\frac{83}{6}\right) + 10$$
- Calculate m∠ABF
Convert 10 to a fraction:
$$10 = \frac{60}{6}$$
Now combine the terms:
$$m\angle ABF = \frac{415}{6} + \frac{60}{6} = \frac{475}{6}$$
This is approximately 79.17 degrees.
$$m\angle ABF = \frac{475}{6} \text{ or } 79.17 \text{ degrees}$$
More Information
The angles on a straight line always add up to 180 degrees. By solving for $x$ with given expressions, we ensure accuracy when calculating the final angle.
Tips
- Not Adding Correctly: Ensure all constant terms are combined.
- Mistakes in Substituting Back: Double-check the substitution into the correct formula for angle ABF.
- Ignoring Simplification: Always simplify fractions where applicable.
AI-generated content may contain errors. Please verify critical information