The curve with equation y = ln x is transformed by a stretch parallel to the x-axis with scale factor 2. Find the equation of the transformed curve.
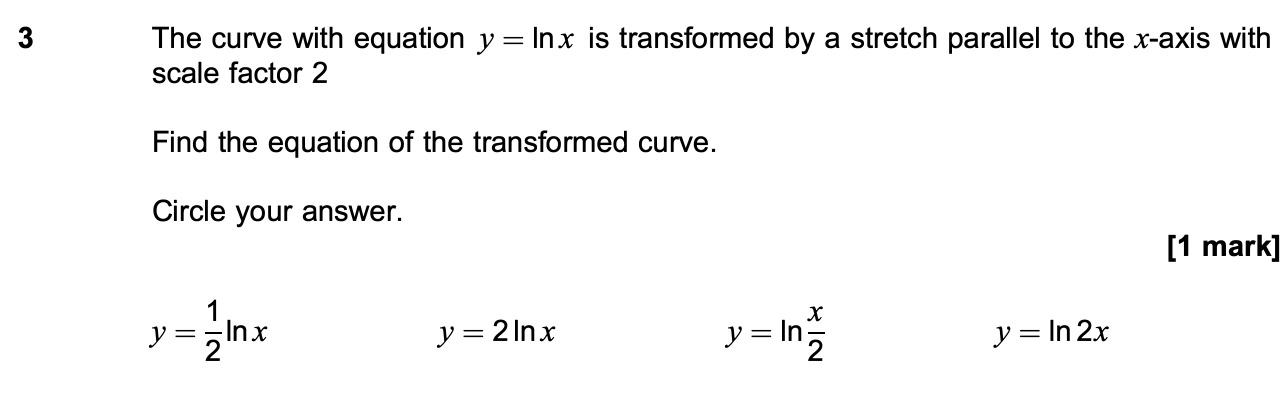
Understand the Problem
The question asks to find the equation of the curve after it has undergone a transformation involving a stretch parallel to the x-axis with a scale factor of 2. This requires applying transformation rules to the original equation.
Answer
The transformed equation is \( y = \ln\left(\frac{x}{2}\right) \).
Answer for screen readers
The equation of the transformed curve is ( y = \ln\left(\frac{x}{2}\right) ).
Steps to Solve
-
Understand the Stretch Transformation A stretch parallel to the x-axis with a scale factor of 2 means that every x-coordinate of the curve will be multiplied by 2.
-
Apply the Transformation to the Original Equation The original equation is given by $y = \ln x$.
To apply the stretch, we replace $x$ with $\frac{x}{2}$ in the equation. This gives us the new equation: $$ y = \ln\left(\frac{x}{2}\right) $$
- Simplify the Transformed Equation Using logarithmic properties, we can simplify the transformed equation: $$ y = \ln\left(\frac{x}{2}\right) = \ln x - \ln 2 $$
Since we need to express the transformed equation in the form provided in the options, we can express it as: $$ y = \ln x - \ln 2 $$
- Identify the Correct Answer from the Given Options Given the options to choose from, we find the one that matches the transformed equation.
The correct option from the list is: $$ y = \ln\left(\frac{x}{2}\right) $$
The equation of the transformed curve is ( y = \ln\left(\frac{x}{2}\right) ).
More Information
This transformation demonstrates the effect of stretching a curve along the x-axis. In this case, the stretch compresses the x-values, thus altering how the logarithmic function behaves.
Tips
- Confusing the stretch parallel to the x-axis with a stretch parallel to the y-axis, which would involve different transformations.
- Not simplifying the transformed equation correctly according to logarithmic rules.
AI-generated content may contain errors. Please verify critical information