For today's exit ticket, Mr. Samuels wants students to graph the inequality y ≥ -1/3x - 4 on the grid below.
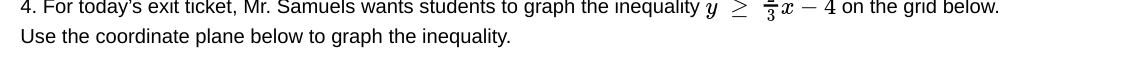
Understand the Problem
The question is asking to graph the inequality y ≥ - rac{1}{3}x - 4 on a provided coordinate plane. The solution will involve identifying the boundary line and determining the shading for the inequality.
Answer
The graph includes a solid line for $y = -\frac{1}{3}x - 4$ with shading above the line for the inequality $y \geq -\frac{1}{3}x - 4$.
Answer for screen readers
The graph of the inequality $y \geq -\frac{1}{3}x - 4$ consists of a solid line representing the boundary $y = -\frac{1}{3}x - 4$ and the area above this line shaded.
Steps to Solve
- Identify the boundary line
To graph the inequality, we first need to graph the boundary line of the equation. The equation of the line is given by
$$ y = -\frac{1}{3}x - 4 $$
- Graph the boundary line
Since we have a "greater than or equal to" ($\geq$) inequality, we will graph the boundary line as a solid line. This indicates that points on the line are included in the solution set.
To plot the line, find two points:
- Find the y-intercept: Set $x = 0$.
$$ y = -\frac{1}{3}(0) - 4 = -4 $$
This gives the point (0, -4).
- Find another point: Set $x = 3$.
$$ y = -\frac{1}{3}(3) - 4 = -1 - 4 = -5 $$
This gives the point (3, -5).
Now, plot the points (0, -4) and (3, -5) on the coordinate plane and draw a solid line through them.
- Determine the shading for the inequality
Since the inequality is $y \geq -\frac{1}{3}x - 4$, we need to shade the region above the line because the values of $y$ that satisfy the inequality are greater than or equal to those on the line.
- Finalizing the graph
Make sure the area above the line is shaded, as this represents all the solutions to the inequality.
The graph of the inequality $y \geq -\frac{1}{3}x - 4$ consists of a solid line representing the boundary $y = -\frac{1}{3}x - 4$ and the area above this line shaded.
More Information
Inequalities can be graphed similarly to equations, but the key is to determine whether the line is solid or dashed. A solid line indicates that points on the line are included in the solution, whereas a dashed line would indicate they are not.
Tips
- Forgetting to use a solid line for "greater than or equal to" ($\geq$).
- Confusing the direction of the shading; always shade above the line for $\geq$.
