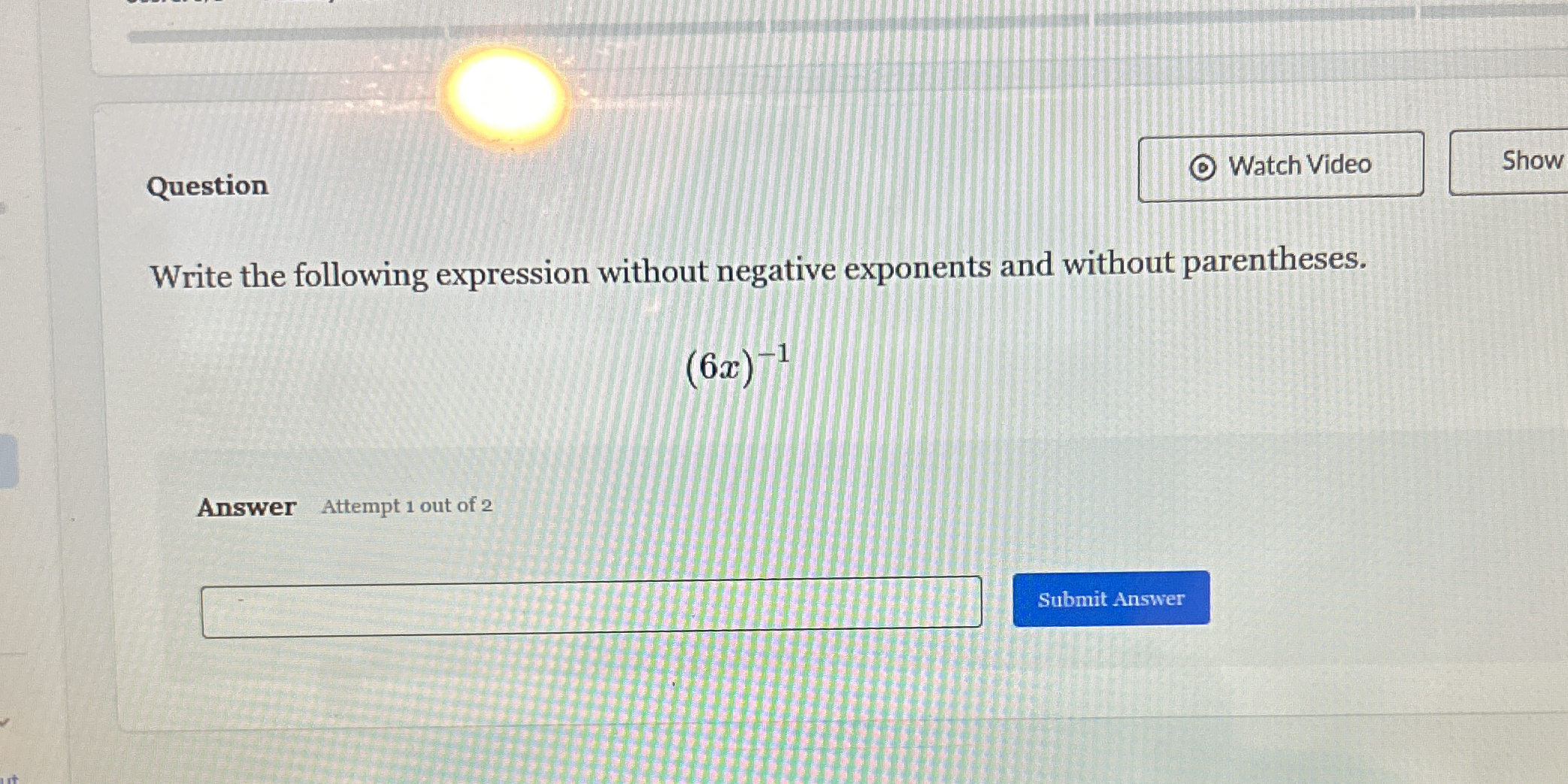
Write the following expression without negative exponents and without parentheses: (6x)^{-1}
Understand the Problem
The question is asking to rewrite the expression (6x)^{-1} in a form that does not have negative exponents and does not use parentheses.
Answer
$$ \frac{1}{6x} $$
Answer for screen readers
The expression without negative exponents and without parentheses is: $$ \frac{1}{6x} $$
Steps to Solve
-
Identify the Negative Exponent The expression given is $(6x)^{-1}$. The negative exponent indicates that we need to take the reciprocal of the base.
-
Apply the Rule for Negative Exponents When an expression has a negative exponent, we can rewrite it as the reciprocal. Thus, we can express $(6x)^{-1}$ as: $$ \frac{1}{6x} $$
-
Remove Parentheses Since we are asked to write the expression without parentheses, we observe that the expression $\frac{1}{6x}$ already meets this requirement.
The expression without negative exponents and without parentheses is: $$ \frac{1}{6x} $$
More Information
This transformation is based on the property of exponents where $a^{-b} = \frac{1}{a^b}$. Understanding this helps in simplifying expressions efficiently.
Tips
-
Forgetting the reciprocal: A common mistake is to leave the negative exponent instead of converting it into a reciprocal. Always remember to change $a^{-1}$ to $\frac{1}{a}$ when simplifying.
-
Leaving parentheses: Ensure that you properly write the final answer without parentheses if specified in the question.
AI-generated content may contain errors. Please verify critical information