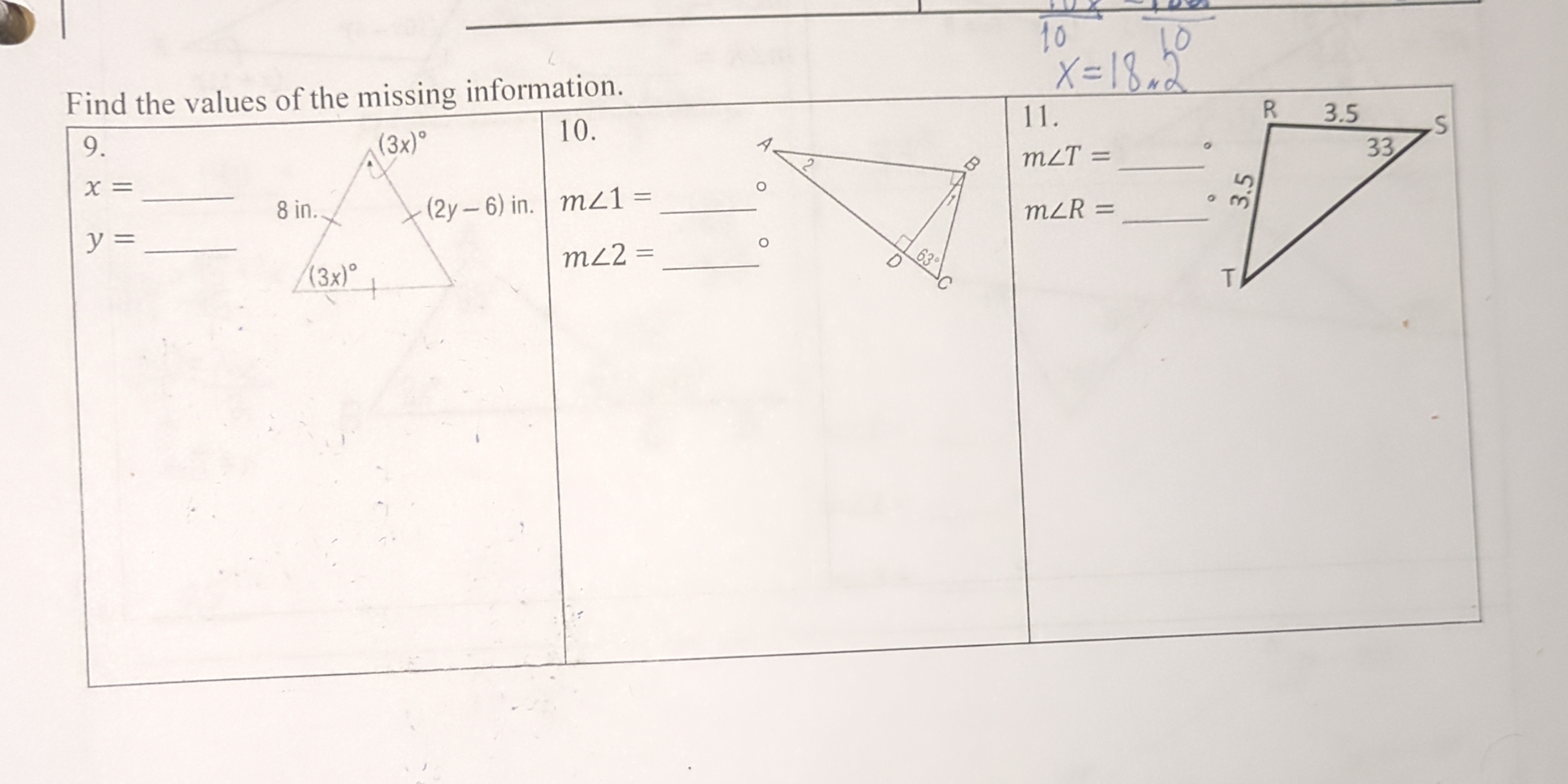
Find the values of the missing information.

Steps to Solve

1. Find the expression for the angles in triangle (Question 9)

The triangle has the following angles:

• The first angle is (3x).
• The second angle is ((2y - 6)^\circ).
• The third angle is ((3x)^\circ).

According to the triangle angle sum property: $$ 3x + (2y - 6) + 3x = 180 $$

This simplifies to: $$ 6x + 2y - 6 = 180 $$

2. Simplify the equation

Rearranging the equation gives us: $$ 6x + 2y = 180 + 6 $$ $$ 6x + 2y = 186 $$

Dividing the entire equation by 2 for simplification: $$ 3x + y = 93 $$ (Equation 1)

3. Find the value of (x)

We know one of the angles is (3x) and the total angle is (180^\circ). Given (x = 18) from earlier findings: Plugging (x) into Equation 1: $$ 3(18) + y = 93 $$ $$ 54 + y = 93 $$

4. Solve for (y)

Now solve for (y): $$ y = 93 - 54 $$ $$ y = 39 $$

5. Find angles in triangle (Question 10)

To find the measures of angles (m\angle 1) and (m\angle 2):

• The triangle has one angle as (63^\circ).
• The remaining angles satisfy: $$ m\angle 1 + m\angle 2 + 63 = 180 $$

6. Use the equation to find the angle measures

Rearranging gives: $$ m\angle 1 + m\angle 2 = 180 - 63 $$ $$ m\angle 1 + m\angle 2 = 117 $$

Assuming (m\angle 1 = x) and (m\angle 2 = y): This creates the equation:

• (x + y = 117) (Equation 2).

The missing specific values for angles will depend on additional info like angle relationships or equality of angles.

7. Move to triangle (Question 11)

For triangle (RST):

• We have angles (m\angle T = 33^\circ) and sides opposite angles (R) and (T) as (3.5) units. Using the triangle sum property again: $$ m\angle R + m\angle T + m\angle S = 180 $$

8. Substituting and solving

Substituting to solve for (m\angle R): $$ m\angle R + 33 + S = 180 $$ Assuming we can derive (S) from the side lengths: $$ m\angle R + S = 147 $$ Similar to the previous triangle, specific angle determination would depend on identifiable relationships.