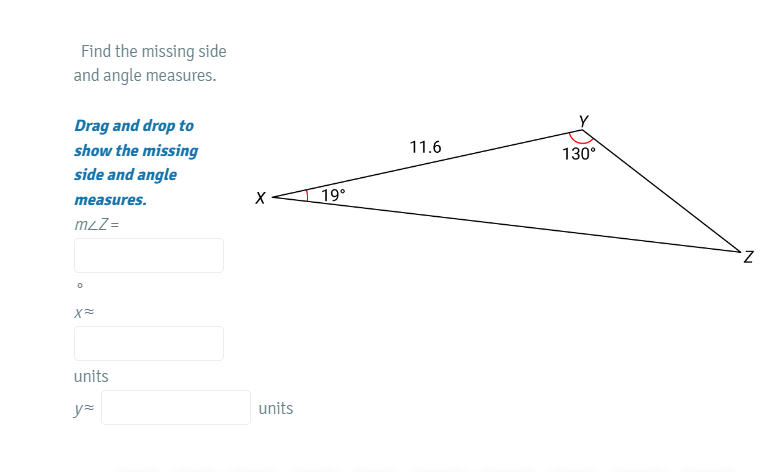
Find the missing side and angle measures of triangle XYZ.

Steps to Solve

1. Find the missing angle
   To find angle $Z$, we can use the fact that the sum of angles in a triangle is $180^\circ$. We know angles $Y$ and $X$, so we calculate:
   $$ m\angle Z = 180^\circ - (m\angle Y + m\angle X) $$
   Substituting the known values:
   $$ m\angle Z = 180^\circ - (130^\circ + 19^\circ) = 180^\circ - 149^\circ = 31^\circ $$

2. Use the Law of Sines to find side $y$
   Now that we have all angles, we can apply the Law of Sines:
   $$ \frac{y}{\sin Y} = \frac{11.6}{\sin Z} $$
   Substituting the known values:
   $$ \frac{y}{\sin(130^\circ)} = \frac{11.6}{\sin(31^\circ)} $$

3. Calculate sin values and solve for $y$
   Using a calculator, we find:
   $$ \sin(130^\circ) \approx 0.766 $$
   $$ \sin(31^\circ) \approx 0.515 $$
   Now we substitute these values in:
   $$ \frac{y}{0.766} = \frac{11.6}{0.515} $$
   Cross-multiplying gives:
   $$ y = 11.6 \cdot \frac{0.766}{0.515} $$
   Calculating, we find:
   $$ y \approx 17.5 $$

4. Use the Law of Sines to find side $x$
   Next, we will find side $x$ using the same Law of Sines formula:
   $$ \frac{x}{\sin X} = \frac{11.6}{\sin Z} $$
   Substituting the known values:
   $$ \frac{x}{\sin(19^\circ)} = \frac{11.6}{\sin(31^\circ)} $$
   Using value for $\sin(31^\circ) \approx 0.515$, we can find $\sin(19^\circ) \approx 0.325$.

5. Calculate $x$ using the values
   $$ \frac{x}{0.325} = \frac{11.6}{0.515} $$
   Cross-multiplying gives:
   $$ x = 11.6 \cdot \frac{0.325}{0.515} $$
   Calculating, we find:
   $$ x \approx 7.38 $$