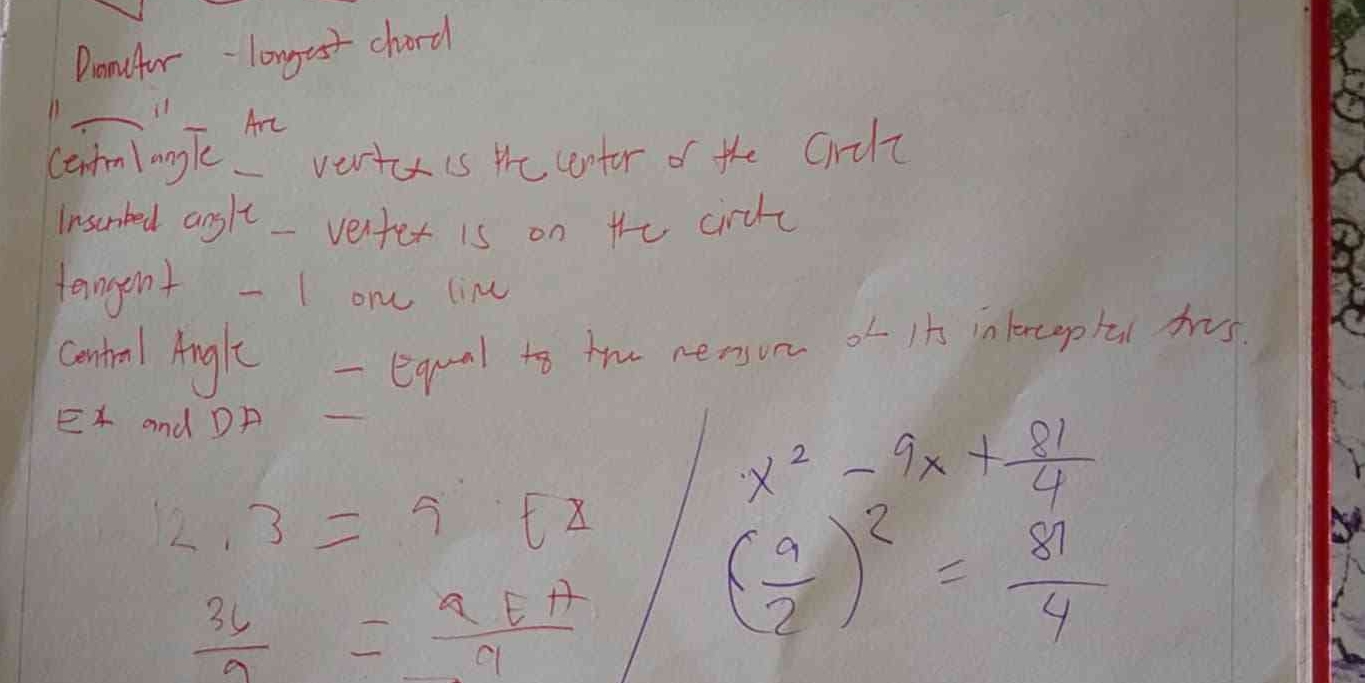
Understand the Problem
The content is related to concepts of circles, including definitions of different types of angles and some equations involving variables. It seems to address properties of angles formed with a circle and their relationship to different geometric elements.
Answer
The solutions are \( x = \frac{3}{5} \), \( A = \frac{1}{2} \), and \( x = 0 \) or \( x = 9 \).
Answer for screen readers
The solutions are ( x = \frac{3}{5} ), ( A = \frac{1}{2} ), and ( x = 0 ) or ( x = 9 ) from the quadratic equation.
Steps to Solve
-
Identifying the elements of the problem The problem involves angles in a circle, where the central angle and inscribed angle are defined, as well as relationships involving a tangent and equations.
-
Setting up the equations From the provided information, we can rewrite the equations based on the relationships of the angles. It appears you have two main equations:
- ( 12, 3 = 9 / x )
- ( \frac{36}{9} = \frac{2}{A} )
-
Solving for ( x ) From the equation ( 12, 3 = 9 / x ), we convert that into a solvable equation:
- This implies ( 12 + 3 = 9 / x ).
- Rearranging gives us ( x = \frac{9}{15} = \frac{3}{5} ).
-
Finding ( A ) from the second equation For the equation ( \frac{36}{9} = \frac{2}{A} ):
- This simplifies to ( 4 = \frac{2}{A} ).
- Cross-multiplying gives ( 4A = 2 ), hence ( A = \frac{2}{4} = \frac{1}{2} ).
-
Solving the quadratic From the quadratic equation ( x^2 - 9x + \frac{81}{4} = \frac{81}{4} ), we simplify this to:
- ( x^2 - 9x = 0 ).
- Factoring gives ( x(x - 9) = 0 ).
- Thus, the solutions are ( x = 0 ) or ( x = 9 ).
The solutions are ( x = \frac{3}{5} ), ( A = \frac{1}{2} ), and ( x = 0 ) or ( x = 9 ) from the quadratic equation.
More Information
These calculations relate to key geometric relationships in a circle, particularly those concerning central and inscribed angles as well as tangent lines.
Tips
- Misinterpreting the relationships between central and inscribed angles.
- Forgetting to properly simplify the equations before solving.
AI-generated content may contain errors. Please verify critical information