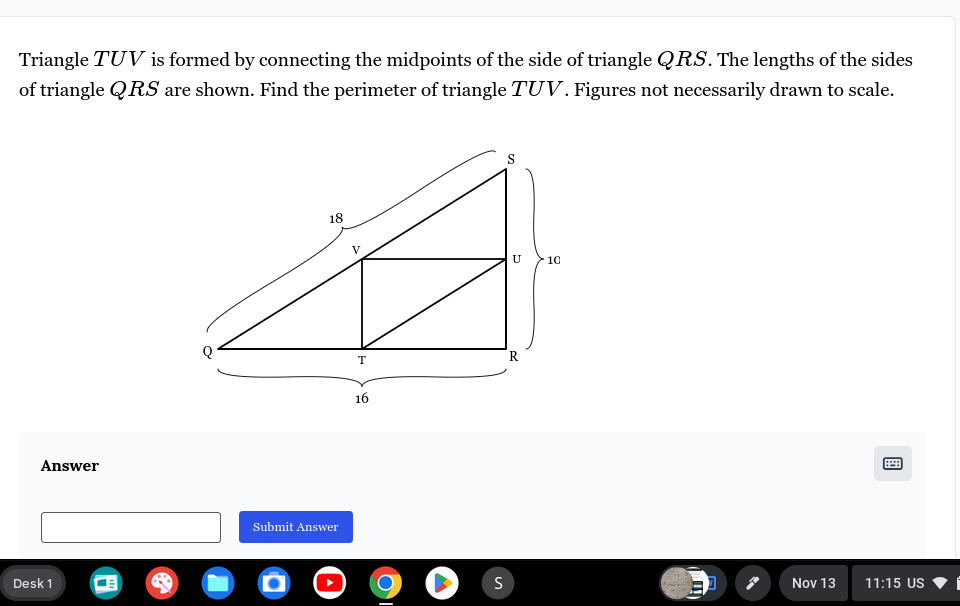
Find the perimeter of triangle TUV.

Understand the Problem

The question is asking for the perimeter of triangle TUV, which is formed by connecting the midpoints of the sides of triangle QRS. Given the lengths of the sides of triangle QRS, we will apply geometric principles to find the lengths of the sides of triangle TUV and then calculate its perimeter.

Answer

The perimeter of triangle TUV is $22$.

Steps to Solve

Identify the sides of triangle QRS

The lengths of the sides of triangle QRS are given:

$QR = 16$
$RS = 18$
$QS = 10$

Determine the lengths of the sides of triangle TUV

Triangle TUV is formed by connecting the midpoints of the sides of triangle QRS. The lengths of the sides of triangle TUV are half the lengths of the sides of triangle QRS:

Length of side $TU = \frac{QR}{2} = \frac{16}{2} = 8$
Length of side $UV = \frac{RS}{2} = \frac{18}{2} = 9$
Length of side $TV = \frac{QS}{2} = \frac{10}{2} = 5$

Calculate the perimeter of triangle TUV

To find the perimeter, we add the lengths of the sides: $$ \text{Perimeter} = TU + UV + TV = 8 + 9 + 5 $$

Sum the side lengths

Calculating the sum: $$ \text{Perimeter} = 8 + 9 + 5 = 22 $$

The perimeter of triangle TUV is $22$.

More Information

Triangle TUV, formed by the midpoints of triangle QRS, has a perimeter that is half the perimeter of triangle QRS. This property is useful in various geometric problems.

Tips

Misunderstanding that the lengths of the sides of triangle TUV are half the lengths of triangle QRS. It's important to remember that midpoints create parallel segments to the base.
Not adding all side lengths correctly; ensure that all sides are included in the total perimeter calculation.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!