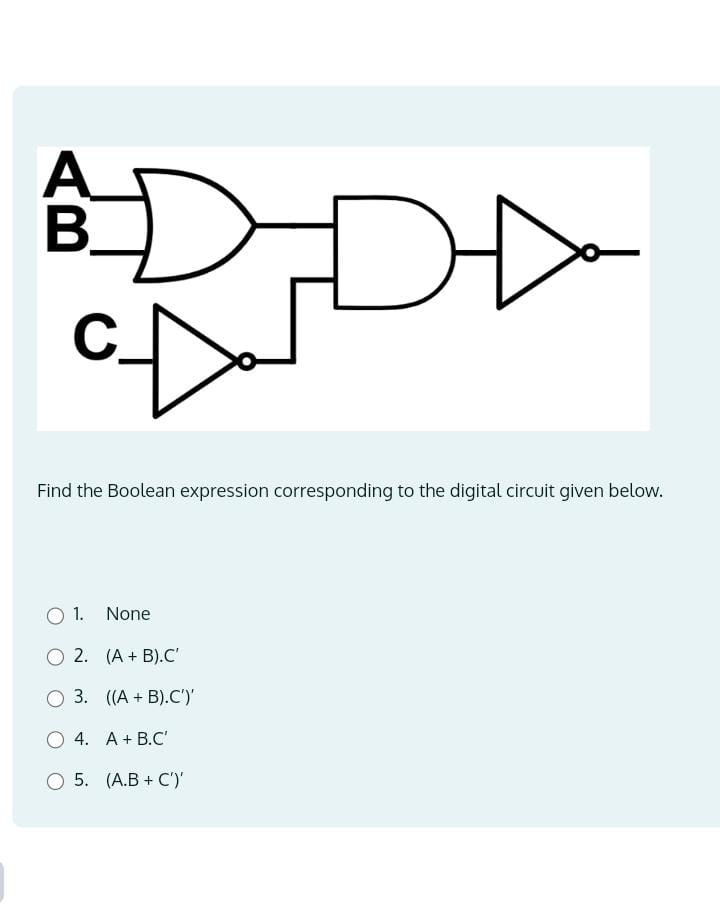
Find the Boolean expression corresponding to the digital circuit given below.
Understand the Problem
The question is asking to determine the Boolean expression that corresponds to a provided digital circuit diagram. This involves analyzing the logical operations performed by the gates in the circuit and expressing that logic in Boolean algebra terms.
Answer
$((A + B)' \cdot C)$
Answer for screen readers
The Boolean expression corresponding to the circuit is: $((A + B)' \cdot C)$
Steps to Solve
-
Identify the Gates in the Circuit First, recognize the logical gates present in the circuit diagram. There are:
- An AND gate (the one combining inputs A, B)
- An OR gate that takes inputs A, B
- Two NOT gates (inverting the outputs of the AND and OR gates)
- A final AND gate that combines these inverted outputs and C.
-
Write the Expression from the OR Gate The expression from the OR gate (taking inputs A and B) is: $$ A + B $$
-
Write the Expression from the AND Gate The expression from the AND gate (taking inputs A and B) is: $$ A \cdot B $$
-
Apply the NOT Gates Now, the output from the OR gate and the AND gate are sent to NOT gates. Therefore:
- The output from the OR gate becomes: $$ (A + B)' $$
- The output from the AND gate becomes: $$ (A \cdot B)' $$
-
Combine Outputs Using AND Gate Finally, both inverted outputs and C are combined using the AND gate. So, the overall expression of the circuit becomes: $$ ((A + B)') \cdot C $$
-
Use De Morgan's Theorem By applying De Morgan's Theorem: $$ (A + B)' = A' \cdot B' $$ So, we substitute and get: $$ (A' \cdot B') \cdot C $$
-
Final Expressions The simplified expression can also be rearranged, resulting in: $$ C \cdot (A' + B') $$
The Boolean expression corresponding to the circuit is: $((A + B)' \cdot C)$
More Information
The expression that combines multiple logic gates represents the output of a digital circuit. Understanding this can help in designing more complex circuits and is fundamental in digital electronics.
Tips
- Misapplying De Morgan's Theorem: Ensure to apply De Morgan's correctly, as it involves converting ANDs to ORs and vice-versa.
- Ignoring NOT Gates: Always pay attention to the inversion effects of NOT gates in the circuit.
AI-generated content may contain errors. Please verify critical information