Given Quadrilateral LMJK is a square. If m∠LMK = (5x + 2y)° and m∠JMK = (11x - y)°, then solve for x and y.
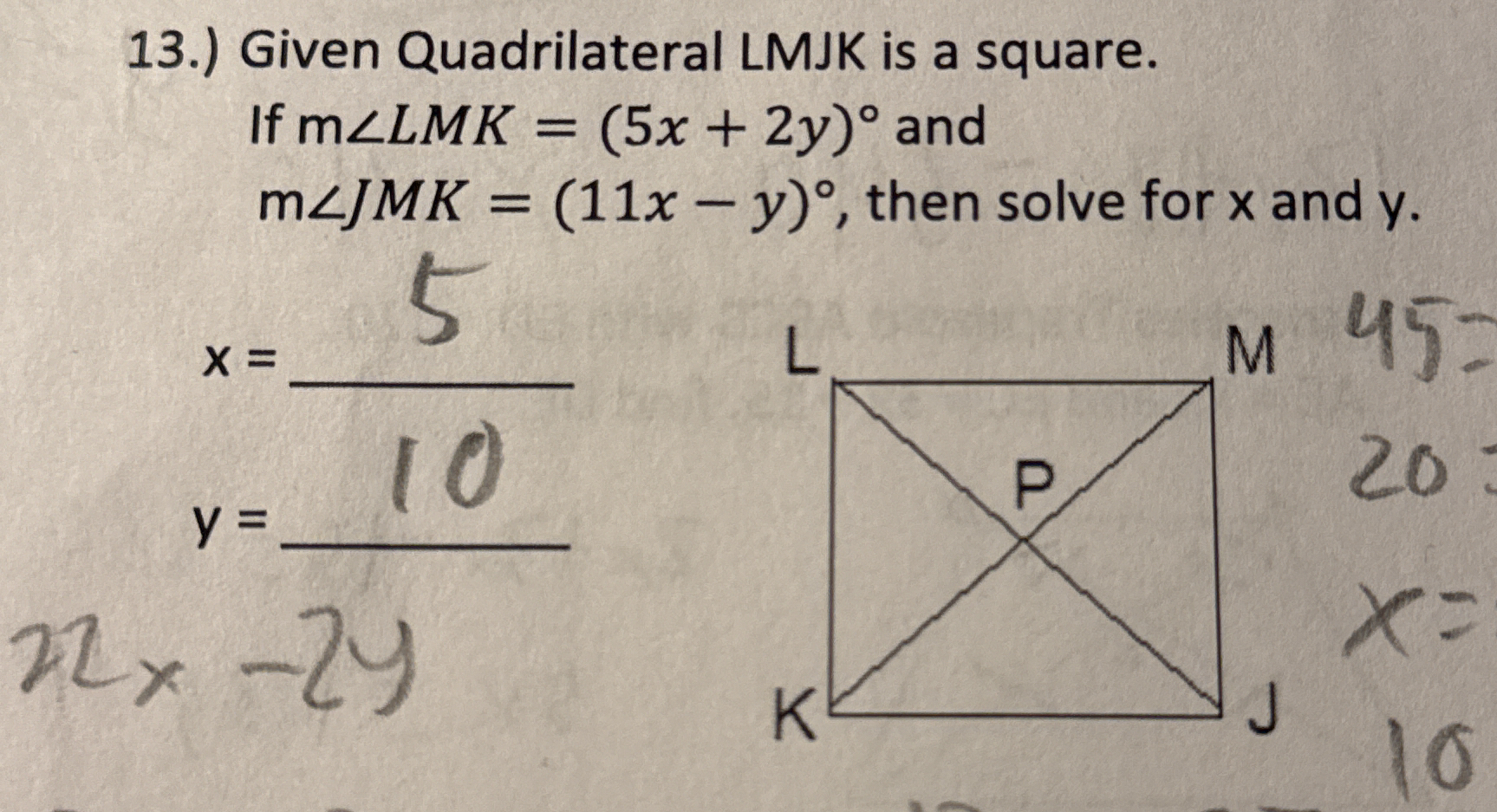
Understand the Problem
The question is asking to solve for the variables x and y based on the angles formed in square LMJK. It provides equations for the measures of angles LMK and JMK, which depend on x and y, and it is necessary to solve these equations within the context of the properties of a square.
Answer
\( x = 10, y = 20 \)
Answer for screen readers
The solution is ( x = 10 ) and ( y = 20 ).
Steps to Solve
-
Identify the angle measures
Since LMJK is a square, we know that each interior angle (including ∠LMK and ∠JMK) measures $90^\circ$. -
Set up the equations
Given:
- $m∠LMK = (5x + 2y)^\circ$
- $m∠JMK = (11x - y)^\circ$
We can set up the following equations based on the property of a square:
$$ 5x + 2y = 90 $$
$$ 11x - y = 90 $$
-
Solve the first equation for y
Rearranging the first equation gives:
$$ 2y = 90 - 5x $$
Thus,
$$ y = \frac{90 - 5x}{2} $$ -
Substitute y into the second equation
Substituting the expression for y into the second equation:
$$ 11x - \left(\frac{90 - 5x}{2}\right) = 90 $$ -
Clear the fraction
Multiply through by 2 to eliminate the fraction:
$$ 2(11x) - (90 - 5x) = 180 $$
This simplifies to:
$$ 22x - 90 + 5x = 180 $$
Combining like terms gives:
$$ 27x - 90 = 180 $$ -
Solve for x
Now, add 90 to both sides:
$$ 27x = 270 $$
Dividing both sides by 27 gives:
$$ x = 10 $$ -
Substitute x back to find y
Now that we have $x$, substitute it back into the equation for $y$:
$$ y = \frac{90 - 5(10)}{2} $$
Calculating the right side gives:
$$ y = \frac{90 - 50}{2} = \frac{40}{2} = 20 $$ -
Final solution
We have found both variables:
- $x = 10$
- $y = 20$
The solution is ( x = 10 ) and ( y = 20 ).
More Information
This problem demonstrates how to use properties of geometry, specifically regarding angles in a square, to form equations and solve for multiple variables. It illustrates algebraic manipulation and substitution.
Tips
Common mistakes include:
- Forgetting that each angle in a square measures $90^\circ$, leading to incorrect equations.
- Mismanaging the arithmetic when clearing fractions or combining terms.
AI-generated content may contain errors. Please verify critical information