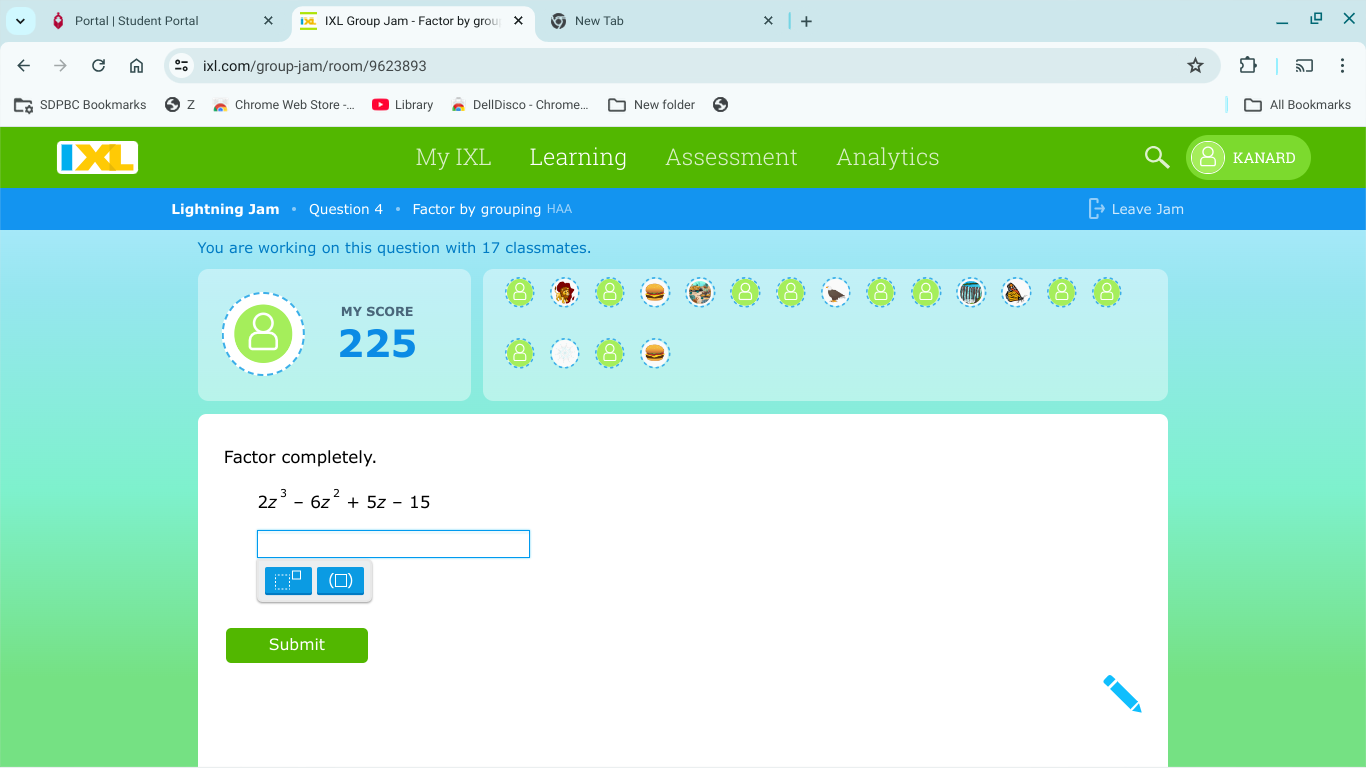
Factor completely. 2z³ - 6z² + 5z - 15
Understand the Problem
The question is asking to factor the polynomial expression completely, specifically the expression 2z³ - 6z² + 5z - 15. This requires identifying common factors and grouping the terms effectively.
Answer
The completely factored form is $$(z - 3)(2z^2 + 5)$$.
Answer for screen readers
The completely factored form of the polynomial $2z^3 - 6z^2 + 5z - 15$ is: $$(z - 3)(2z^2 + 5)$$
Steps to Solve
-
Identify common factors in pairs Group the terms as follows: $$ (2z^3 - 6z^2) + (5z - 15) $$
-
Factor out the common factors From the first group, factor out $2z^2$, and from the second group, factor out $5$: $$ 2z^2(z - 3) + 5(z - 3) $$
-
Factor by grouping Now, notice that $(z - 3)$ is a common factor: $$ (z - 3)(2z^2 + 5) $$
-
Final expression The completely factored form of the polynomial is: $$ (z - 3)(2z^2 + 5) $$
The completely factored form of the polynomial $2z^3 - 6z^2 + 5z - 15$ is: $$(z - 3)(2z^2 + 5)$$
More Information
Factoring is a fundamental skill in algebra that helps simplify expressions. The technique of grouping allows for pulling out common factors and can also be used for more complex polynomials.
Tips
- Forgetting to group both pairs correctly can lead to missing the common factor.
- Not factoring out the greatest common factor (GCF) can also result in an incorrect factorization.
- Skipping the verification step; you should always check by redistributing to ensure accuracy.
AI-generated content may contain errors. Please verify critical information