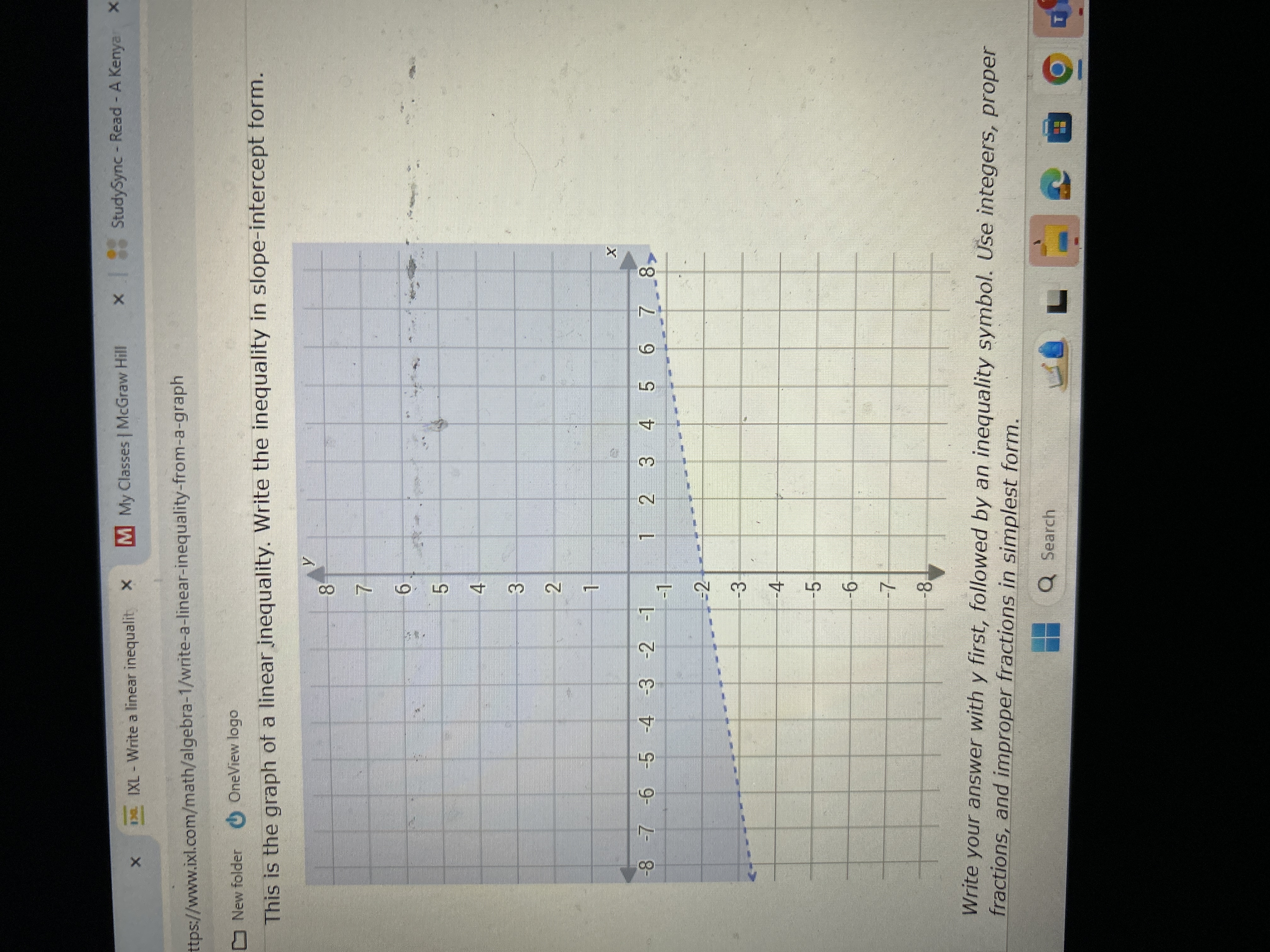
This is the graph of a linear inequality. Write the inequality in slope-intercept form.
Understand the Problem
The question is asking for the inequality representation of the linear graph provided. It requires identifying the slope and y-intercept to write the inequality in slope-intercept form (y < mx + b or y > mx + b).
Answer
$$ y < x - 2 $$
Answer for screen readers
The inequality representation is:
$$ y < x - 2 $$
Steps to Solve
- Identify the slope and y-intercept of the line
The graph shows a dashed line. For a dashed line, the inequality will be strict (either $<$ or $>$). Identify two points on the line to calculate the slope (m). For example, using points at $(1, 2)$ and $(3, 4)$:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - 2}{3 - 1} = \frac{2}{2} = 1 $$
- Find the y-intercept
Look for where the line crosses the y-axis. In this case, it appears to cross at $-2$:
$$ b = -2 $$
So we have the slope $m = 1$ and the y-intercept $b = -2$.
- Write the inequality in slope-intercept form
Using the slope-intercept form $y = mx + b$, substitute the values of $m$ and $b$. The equation of the line becomes:
$$ y = 1x - 2 $$
Since the graph has a dashed line, it indicates a strict inequality. Therefore, we write:
$$ y < x - 2 $$
The inequality representation is:
$$ y < x - 2 $$
More Information
The equation represents a boundary line where the values of $y$ are less than those on the line, indicating the region below the line on the graph.
Tips
- Confusing a dashed line with a solid line. A dashed line indicates that the points on the line are not included in the solution set.
- Miscalculating the slope by incorrectly identifying points on the line.
AI-generated content may contain errors. Please verify critical information