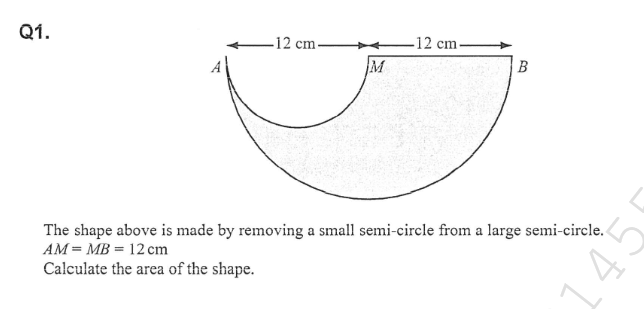
Calculate the area of the shape formed by removing a small semi-circle from a large semi-circle.
Understand the Problem
The question is asking to calculate the area of a shape formed by removing a small semicircle from a large semicircle. The base of the large semicircle (AM and MB) measures 12 cm each, so the entire diameter is 24 cm. The task requires determining the area of the resulting shape after the removal of the small semicircle.
Answer
The area of the shape is $54\pi \text{ cm}^2$.
Answer for screen readers
The area of the shape is $54\pi \text{ cm}^2$.
Steps to Solve
- Identify the dimensions of the semicircles
The large semicircle has a diameter of $24 \text{ cm}$, hence its radius $R$ is calculated as follows: $$ R = \frac{24}{2} = 12 \text{ cm} $$
The small semicircle has a diameter of $12 \text{ cm}$, thus its radius $r$ is: $$ r = \frac{12}{2} = 6 \text{ cm} $$
- Calculate the area of the large semicircle
The area $A_L$ of a semicircle is given by the formula: $$ A_L = \frac{1}{2} \pi R^2 $$
Substituting in the radius of the large semicircle: $$ A_L = \frac{1}{2} \pi (12)^2 = \frac{1}{2} \pi \times 144 = 72\pi \text{ cm}^2 $$
- Calculate the area of the small semicircle
Using the same formula for the small semicircle: $$ A_S = \frac{1}{2} \pi r^2 $$
Substituting in the radius of the small semicircle: $$ A_S = \frac{1}{2} \pi (6)^2 = \frac{1}{2} \pi \times 36 = 18\pi \text{ cm}^2 $$
- Determine the area of the resulting shape
The area of the shape formed after removing the small semicircle from the large semicircle is: $$ A_{result} = A_L - A_S $$
Substituting the areas calculated: $$ A_{result} = 72\pi - 18\pi = 54\pi \text{ cm}^2 $$
The area of the shape is $54\pi \text{ cm}^2$.
More Information
The area calculated represents the remaining part of the large semicircle after removing the smaller one. The use of $\pi$ indicates that the area is a product of the important geometric constant, approximately equal to $3.14$.
Tips
- Confusing between the diameters and radii when calculating areas of semicircles.
- Failing to subtract the area of the small semicircle from that of the large semicircle.
AI-generated content may contain errors. Please verify critical information