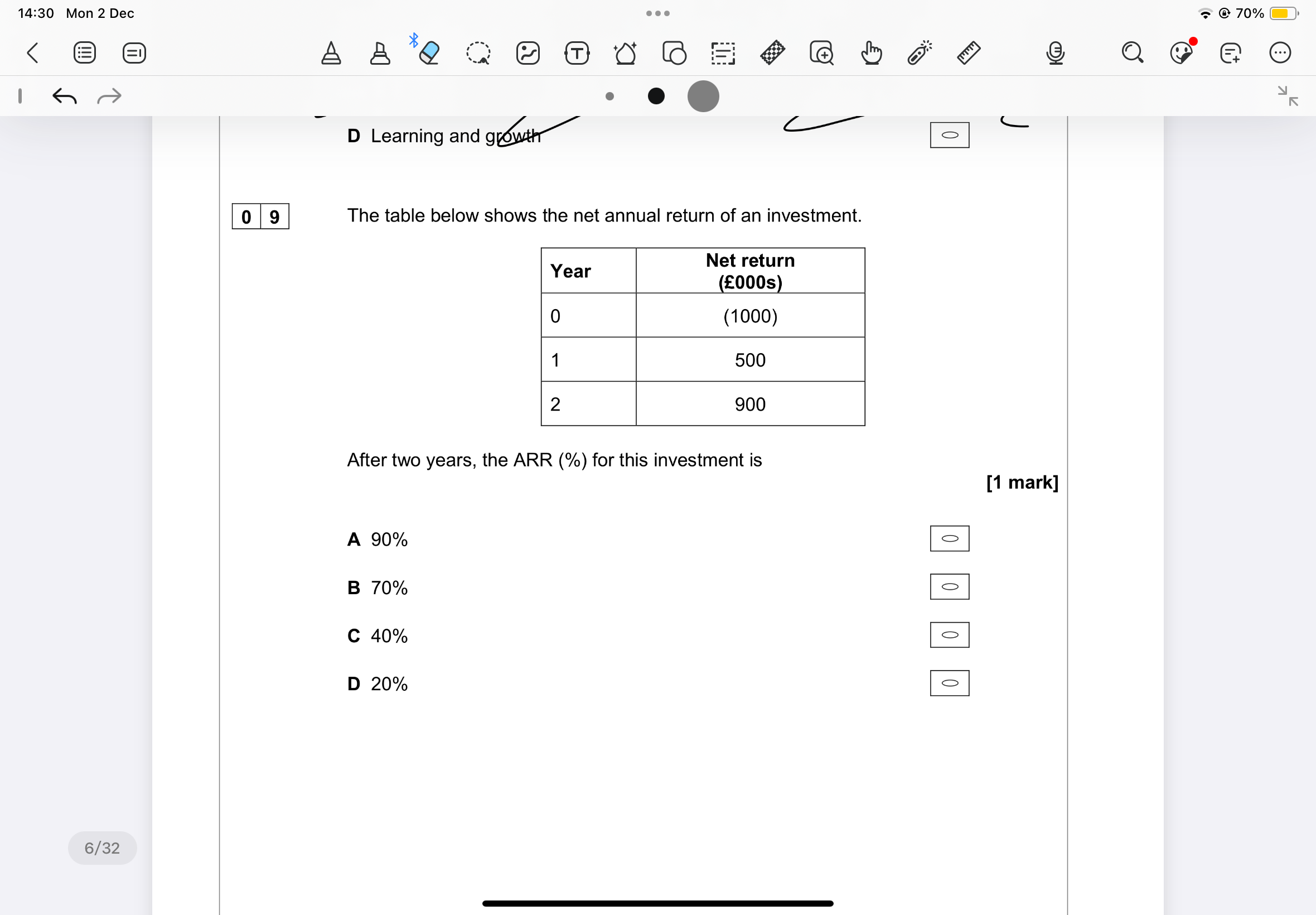
After two years, the ARR (%) for this investment is?
Understand the Problem
The question is asking to calculate the Average Rate of Return (ARR) for an investment over two years, based on the given net returns for those years. It requires an understanding of basic financial metrics to derive the percentage return from the values provided.
Answer
The ARR is \( 40\% \).
Answer for screen readers
The Average Rate of Return (ARR) is ( 40% ).
Steps to Solve
- Identify Total Net Returns
First, calculate the total net returns over the investment period. The total returns can be found by summing the returns from each year:
$$ \text{Total Net Return} = \text{Net Return in Year 1} + \text{Net Return in Year 2} - \text{Net Return in Year 0} $$
Substituting the values from the table:
$$ \text{Total Net Return} = 500 + 900 - 1000 = 400 $$
- Calculate Average Annual Return
Next, to find the Average Annual Return (ARR), you divide the total net return by the number of years and then divide by the initial investment:
$$ \text{ARR} = \left( \frac{\text{Total Net Return}}{\text{Initial Investment}} \right) \times 100 $$
Here, the initial investment is £1000 (which is negative as it's an outflow):
$$ \text{ARR} = \left( \frac{400}{1000} \right) \times 100 = 40% $$
- Final Result
The calculated ARR is 40%. Hence, the final answer is
$$ \text{ARR} = 40% $$
The Average Rate of Return (ARR) is ( 40% ).
More Information
The ARR represents the percentage return on an investment averaged over a specific time period. In this case, over two years, the investment provided a return of £400 on an initial investment of £1000.
Tips
null
AI-generated content may contain errors. Please verify critical information