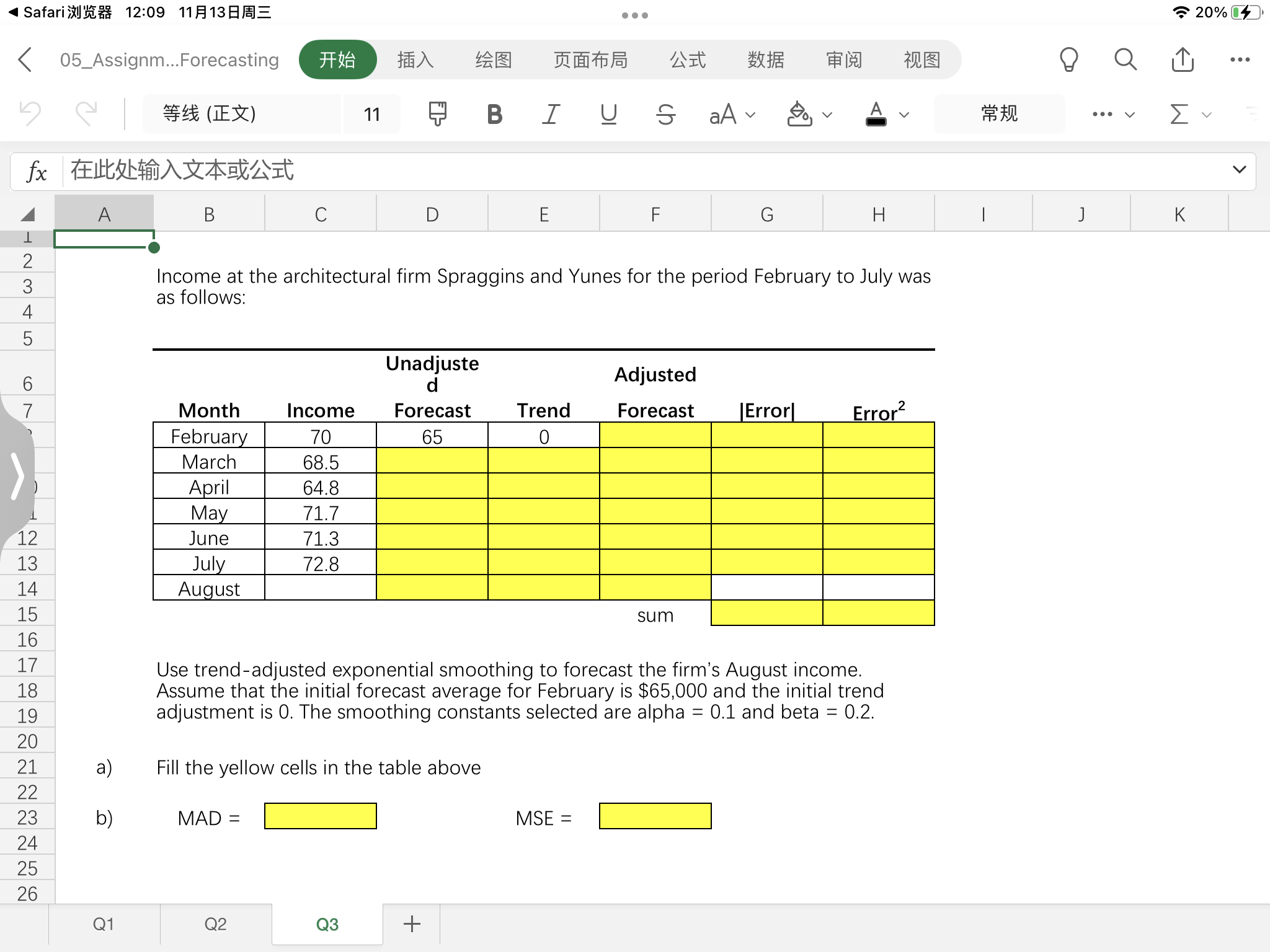
Use trend-adjusted exponential smoothing to forecast the firm's August income. Assume that the initial forecast average for February is $65,000 and the initial trend adjustment is... Use trend-adjusted exponential smoothing to forecast the firm's August income. Assume that the initial forecast average for February is $65,000 and the initial trend adjustment is 0. The smoothing constants selected are alpha = 0.1 and beta = 0.2. Fill the yellow cells in the table above. MAD = MSE = Read more

Steps to Solve

1. Calculate Adjusted Forecast for Each Month

Using the trend-adjusted exponential smoothing formula: $$ \text{Adjusted Forecast} = \text{Forecast} + \text{Trend} $$ For each month from February to July, use the previous month's adjusted forecast and update it accordingly. Start with February's forecast of 65.

2. Calculate Trend for Each Month

To update the trend, use: $$ \text{Trend} = \beta \times (\text{Adjusted Forecast} - \text{Forecast}) + (1 - \beta) \times \text{Trend} $$ Start with an initial trend of 0, and apply this formula for each subsequent month.

3. Compute the Error for Each Month

Calculate the error for each month using: $$ \text{Error} = \text{Income} - \text{Adjusted Forecast} $$ Record the error values in the appropriate column.

4. Calculate Error Squared for Each Month

For each month, compute the squared error: $$ \text{Error}^2 = \text{Error}^2 $$ Update the table with these values.

5. Forecast August Income

For August, the adjusted forecast can be computed using February to July data with: $$ \text{Adjusted Forecast (August)} = \text{Adjusted Forecast (July)} + \text{Trend (July)} $$

6. Calculate MAD (Mean Absolute Deviation)

MAD is calculated using: $$ \text{MAD} = \frac{\sum |\text{Error}|}{n} $$ where (n) is the number of months (6 months from February to July). Calculate the sum of the absolute errors.

7. Calculate MSE (Mean Squared Error)

MSE is calculated using: $$ \text{MSE} = \frac{\sum \text{Error}^2}{n} $$ where (n) is again the number of months. Sum up the squared errors and divide by 6.