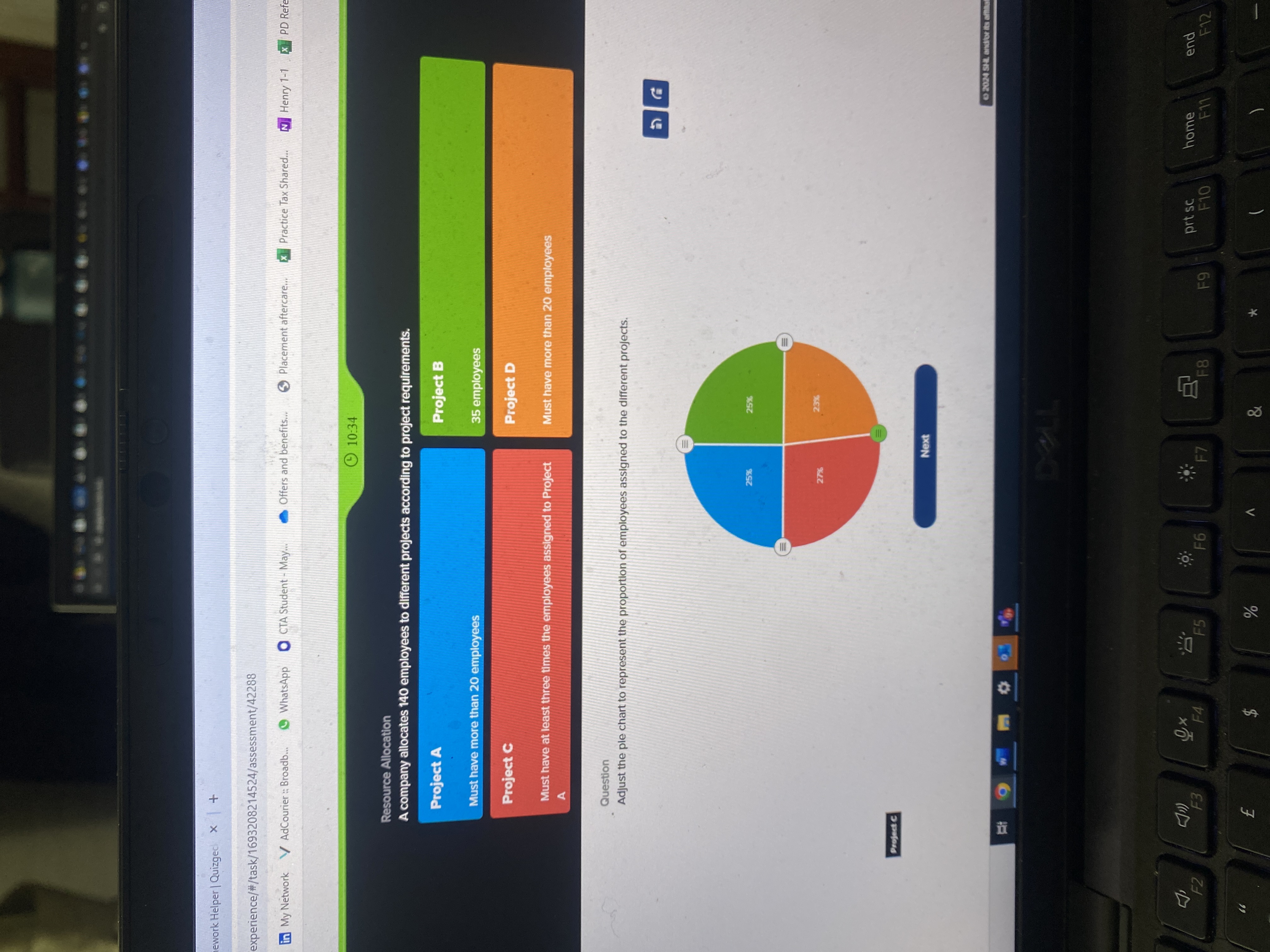
Adjust the pie chart to represent the proportion of employees assigned to the different projects.

Steps to Solve

1. Define the total number of employees
   The company has a total of 140 employees that need to be allocated across the projects.

2. Assign Project B employees
   Project B requires 35 employees.
   So, remaining employees = $140 - 35 = 105$ employees.

3. Allocate for Projects A, C, and D
   Project A must have more than 20 employees. Let's denote the number of employees assigned to Project A as $x$.

4. Determine the relationship for Project C
   Project C must have at least three times the employees assigned to Project A. Therefore, if Project A has $x$ employees, Project C must have at least $3x$ employees.

5. Determine the relationship for Project D
   Project D must have more than 20 employees. Let’s denote the number of employees assigned to Project D as $y$.
   We now have the equation:

$$ x + 3x + y = 105 $$

Which simplifies to:

$$ 4x + y = 105 $$

6. Set inequalities
   From the requirements, we have:

• $x > 20$ (Project A)
• $y > 20$ (Project D)

7. Solve for the range of $x$
   From the equation $y = 105 - 4x$, we also have $y > 20$:

$$ 105 - 4x > 20 $$ $$ 85 > 4x $$ $$ \frac{85}{4} > x $$
This simplifies to:

$$ x < 21.25 $$

Thus, the possible integer values for $x$ are 21, since $x > 20$.

8. Calculate employees for Projects C and D
   If ( x = 21: )

$$ 3x = 3(21) = 63 \text{ (Project C)} $$
Then, we calculate ( y ):

$$ y = 105 - 4(21) = 105 - 84 = 21 \text{ (Project D)} $$

9. Final distribution of employees
   With these assignments, we have the following:

• Project A: 21 employees
• Project B: 35 employees
• Project C: 63 employees
• Project D: 21 employees

10. Calculate proportions for the pie chart
    To find the percentages for the pie chart, calculate:

• Project A: $\frac{21}{140} \times 100 \approx 15%$
• Project B: $\frac{35}{140} \times 100 = 25%$
• Project C: $\frac{63}{140} \times 100 \approx 45%$
• Project D: $\frac{21}{140} \times 100 \approx 15%$

This gives us a final distribution for the pie chart.