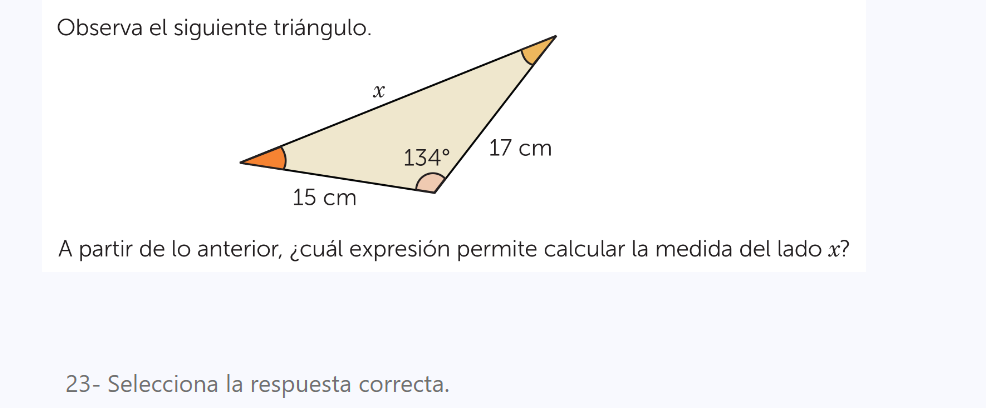
A partir de lo anterior, ¿cuál expresión permite calcular la medida del lado x?
Understand the Problem
La pregunta está pidiendo identificar qué expresión se puede usar para calcular la medida del lado x en un triángulo dado, donde se proporcionan ciertas medidas y un ángulo. Se requiere aplicar conceptos relacionados con las propiedades de los triángulos, posiblemente el teorema del seno o del coseno.
Answer
La expresión para calcular el lado $x$ es: $$ x = \sqrt{15^2 + 17^2 - 2 \cdot 15 \cdot 17 \cdot \cos(134^\circ)} $$
Answer for screen readers
La expresión que permite calcular la medida del lado $x$ es: $$ x = \sqrt{15^2 + 17^2 - 2 \cdot 15 \cdot 17 \cdot \cos(134^\circ)} $$
Steps to Solve
-
Identificar los elementos del triángulo El triángulo dado tiene un lado 17 cm, otro lado 15 cm y un ángulo de $134^\circ$. Queremos encontrar el lado $x$ opuesto a ese ángulo.
-
Aplicar la Ley de los Cosenos Para calcular la longitud del lado $x$, podemos usar la Ley de los Cosenos, que se expresa como: $$ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) $$ donde:
- $c$ es el lado opuesto al ángulo $C$ (en este caso, $x$).
- $a$ y $b$ son los otros dos lados del triángulo (15 cm y 17 cm).
- $C$ es el ángulo entre los lados $a$ y $b$ (en este caso, $134^\circ$).
-
Escribir la expresión utilizando la Ley de los Cosenos Sustituyendo los valores en la fórmula, obtenemos: $$ x^2 = 15^2 + 17^2 - 2 \cdot 15 \cdot 17 \cdot \cos(134^\circ) $$
-
Calcular la medida del lado x Ahora, podemos despejar $x$: $$ x = \sqrt{15^2 + 17^2 - 2 \cdot 15 \cdot 17 \cdot \cos(134^\circ)} $$
La expresión que permite calcular la medida del lado $x$ es: $$ x = \sqrt{15^2 + 17^2 - 2 \cdot 15 \cdot 17 \cdot \cos(134^\circ)} $$
More Information
La Ley de los Cosenos es especialmente útil para calcular lados de triángulos cuando se conoce un ángulo y los lados adyacentes. Este tipo de problema es común en geometría, y fortalecer el entendimiento de la Ley es esencial para resolver triángulos no rectángulos.
Tips
- No identificar correctamente el ángulo opuesto al lado que queremos calcular.
- Usar la Ley de los Senos en lugar de la Ley de los Cosenos, ya que aquí tenemos un triángulo donde se conoce un ángulo y dos lados.
AI-generated content may contain errors. Please verify critical information