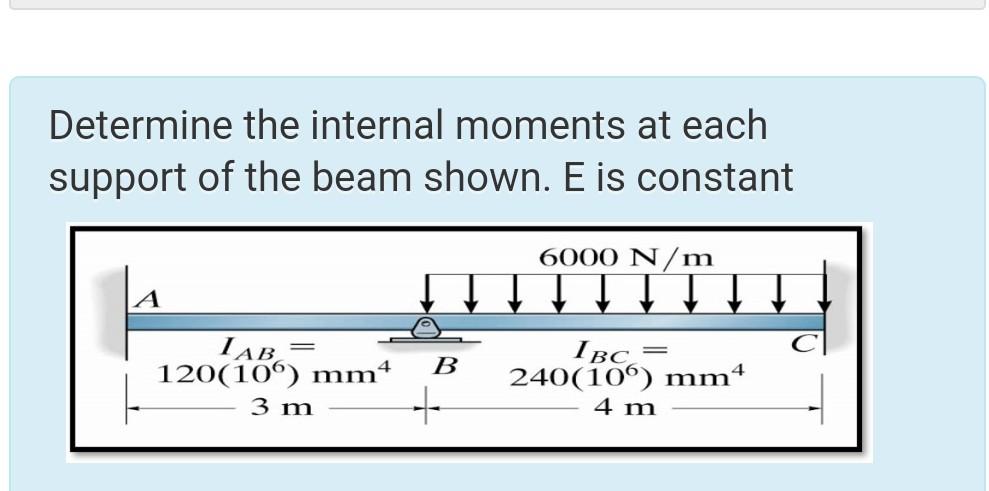
Determine the internal moments at each support of the beam shown. E is constant.

Steps to Solve

1. Identify the Loads and Supports

The beam has a uniformly distributed load of $6000 , \text{N/m}$ and is supported at points A and C. We will analyze the forces acting on the system.

2. Calculate Total Load

The total load on the beam can be found using the formula: $$ P = w \times L $$ where $w = 6000 , \text{N/m}$ and ( L = 7 , \text{m} ) (total span from A to C).

Calculating: $$ P = 6000 , \text{N/m} \times 7 , \text{m} = 42000 , \text{N} $$

3. Determine Reaction Forces at Supports

Using static equilibrium (sum of vertical forces = 0): Let ( R_A ) be the reaction force at A and ( R_C ) at C.

The total load downward must equal the total upward forces: $$ R_A + R_C = P $$ Thus, $$ R_A + R_C = 42000 , \text{N} \tag{1} $$

To find moments, take moments around support A: $$ \sum M_A = 0 $$ The moment due to the total load: $$ 6000 \times 7 - R_C \times 7 = 0 $$ Solving for ( R_C ): $$ 42000 - 7R_C = 0 $$ $$ R_C = \frac{42000}{7} = 6000 , \text{N} $$

4. Calculate Reaction at A

Using equation (1): $$ R_A + 6000 = 42000 $$ Solving for ( R_A ): $$ R_A = 42000 - 6000 = 36000 , \text{N} $$

5. Determine Internal Moments at Supports

Using the calculated reactions:

• The internal moment at support A is zero since it’s a pinned support.
• The internal moment at support C can be calculated by taking the moment about A or C due to the loads.

Using the reaction force at C: The internal moment at C due to external load can be calculated as: For distributed load, overall moment: $$ M_C = -\frac{1}{2} \times P \times d $$ Where ( d ) is the distance to center of load from C: $$ d = \frac{L}{2} = 3.5 , \text{m} $$ Thus, $$ M_C = -\frac{1}{2} \times 42000 \times 3.5 = -73500 , \text{N} \cdot \text{m} $$