7x - 1 - 1(4x - 1 - x) = 10/3
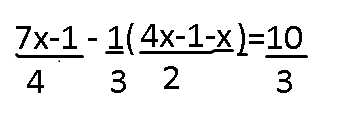
Understand the Problem
The question is asking us to solve the equation involving fractions and simplification. To solve it, we will perform steps to isolate the variable x.
Answer
The value of $x$ is $\frac{13}{3}$.
Answer for screen readers
The solution to the equation is:
$$ x = \frac{13}{3} $$
Steps to Solve
- Rewrite the equation for clarity
Start with the equation:
$$ \frac{7x - 1}{4} - \frac{1}{3}(4x - 1 - x) = \frac{10}{3} $$
- Distribute the fraction
Distribute the $\frac{1}{3}$ to the terms inside the parentheses:
$$ \frac{7x - 1}{4} - \left(\frac{4x}{3} - \frac{1}{3} - \frac{x}{3}\right) = \frac{10}{3} $$
This simplifies to:
$$ \frac{7x - 1}{4} - \left(\frac{4x - x}{3} - \frac{1}{3}\right) = \frac{10}{3} $$
Which further reduces to:
$$ \frac{7x - 1}{4} - \left(\frac{3x - 1}{3}\right) = \frac{10}{3} $$
- Get a common denominator
To simplify the equation further, find a common denominator for the left side:
The common denominator between 4 and 3 is 12.
Rewrite the fractions:
$$ \frac{3(7x - 1)}{12} - \frac{4(3x - 1)}{12} = \frac{10}{3} $$
- Combine the fractions
Now combine the fractions on the left side:
$$ \frac{3(7x - 1) - 4(3x - 1)}{12} = \frac{10}{3} $$
Distributing gives us:
$$ \frac{21x - 3 - 12x + 4}{12} = \frac{10}{3} $$
Simplifying the numerator:
$$ \frac{9x + 1}{12} = \frac{10}{3} $$
- Eliminate the fraction by multiplying
Multiply both sides by 12 to eliminate the denominator:
$$ 9x + 1 = 40 $$
- Isolate x
Subtract 1 from both sides:
$$ 9x = 39 $$
Now divide by 9:
$$ x = \frac{39}{9} = \frac{13}{3} $$
The solution to the equation is:
$$ x = \frac{13}{3} $$
More Information
This means that when $x$ is approximately 4.33, the original equation holds true. This type of equation is common in algebra and helps develop skills for handling fractions and variables.
Tips
- Forgetting to distribute the fraction correctly.
- Failing to find a common denominator.
- Miscalculating while combining like terms in the numerators.
AI-generated content may contain errors. Please verify critical information