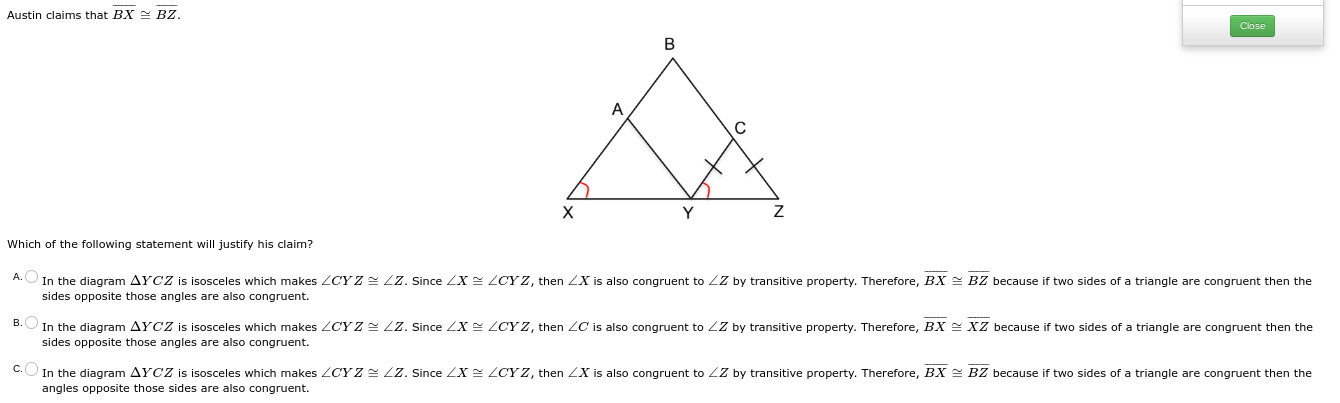
Which of the following statement will justify his claim?
Understand the Problem
The question is asking which statement correctly justifies Austin's claim that the segments BX and BZ are congruent based on the properties of triangles and angles. The answer involves identifying the correct reasoning related to isosceles triangles and congruency.
Answer
C: In the diagram $\triangle YCZ$ is isosceles which makes $\angle CYZ \cong \angle Z$. Since $\angle X \cong \angle CYZ$, then $\overline{BX} \cong \overline{BZ}$.
Answer for screen readers
The correct justification is:
C. In the diagram $\triangle YCZ$ is isosceles which makes $\angle CYZ \cong \angle Z$. Since $\angle X \cong \angle CYZ$, then $\angle X$ is also congruent to $\angle Z$ by transitive property. Therefore, $\overline{BX} \cong \overline{BZ}$ because if two sides of a triangle are congruent then the angles opposite those sides are also congruent.
Steps to Solve
-
Identify the Triangle Properties The triangle $\triangle YCZ$ is isosceles, meaning two sides are equal, and the angles opposite those sides are also equal.
-
Determine the Angles We know that $\angle X \cong \angle CYZ$ which is provided in the problem. Since $\triangle YCZ$ is isosceles, this means the two angles opposite the equal sides ($CY$ and $CZ$) are equal.
-
Use Transitive Property If $\angle X \cong \angle CYZ$, then by the transitive property of equality, $\angle X$ is also congruent to the angle opposite $BZ$.
-
Conclusion on Sides Since the angles $\angle X$ and $\angle CYZ$ are congruent, and the triangles are isosceles, it follows that the sides opposite these angles, $BX$ and $BZ$, are also congruent. Thus, we have $BX \cong BZ$.
The correct justification is:
C. In the diagram $\triangle YCZ$ is isosceles which makes $\angle CYZ \cong \angle Z$. Since $\angle X \cong \angle CYZ$, then $\angle X$ is also congruent to $\angle Z$ by transitive property. Therefore, $\overline{BX} \cong \overline{BZ}$ because if two sides of a triangle are congruent then the angles opposite those sides are also congruent.
More Information
This reasoning is based on the properties of isosceles triangles, where if two angles are equal, the sides opposite those angles are also equal. This is a crucial concept in triangle congruency and properties.
Tips
- Confusing the angles and sides: Always remember that angles opposite equal sides are equal in isosceles triangles.
- Misapplying the transitive property: Ensure that the relationships between angles and their opposite sides are correctly understood.
AI-generated content may contain errors. Please verify critical information